Exercice de maths de terminale sur la géométrie dans l’espace : vecteur, cube, triangle, centre de gravité, égalité, alignement, parallélisme.
Exercice N°227 :
ABCDEFGH est un cube, I est le milieu du segment [BD] et K est le centre de gravité du triangle BGD (c’est à dire que →GK = (2/3)→GI).
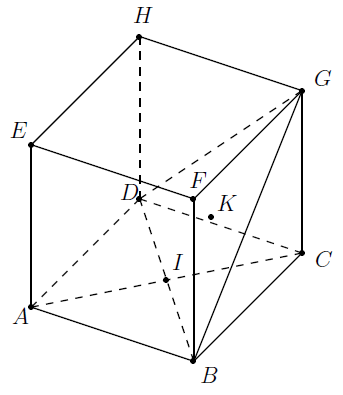
1) Montrer que →IK = (1/3)→IC + (1/3)→AE.
2) Exprimer le vecteur →IC en fonction de →AB et →AD.
3) Exprimer alors le vecteur →AK en fonction des vecteurs →AB, →AD et →AE.
On munit l’espace du repère (A, →AB, →AD, →AE).
4) Déterminer les coordonnées des points E, C et K dans ce repère.
5) Montrer que les points E, C et K sont alignés.
Soit J le point tel que →EJ = (2/3)→EH + (2/3)→AF.
6) Montrer que les droites (KJ) et (AE) sont parallèles.
7) Soit M(3 ; 3 ; -1).
Montrer que le point M appartient au plan (ACE).
Bon courage,
Sylvain Jeuland
Pour avoir le corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de ce chapitre (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés de l’exercice : géométrie, espace, vecteur, cube.
Exercice précédent : Géométrie 3D – Sécantes, parallèles, coplanaires – Terminale

