Maths de première : exercice de fonction rationnelle et second degré. Numérateur, dénominateur, courbe, signe, tableau de valeurs.
Exercice N°383 :

Exercice N°383 :
Soit f la fonction définie par :
f(x) = (-x2 + 2x + 3)/(2x2 – 4x + 6).
1) Montrer que la fonction f est définie sur R.
On nomme Cf sa courbe représentative dans un repère orthogonal (O , →i , →j).
2) Montrer que Cf coupe l’axe des abscisses (Ox) en deux points dont on calculera les coordonnées.
3) Montrer que, pour tout x ∈ R
f(x) ≤ 1.
4) Quelle interprétation peut-on faire de ce résultat ?
5) Dresser le tableau de signe du numérateur puis celui du dénominateur de la fonction f sur R.
6) En déduire le signe de f sur R.
7) Compléter le tableau de valeurs de f sur l’intervalle [−3 ; 4] ci-dessous.

On arrondira toutes les valeurs à 10−2 près.
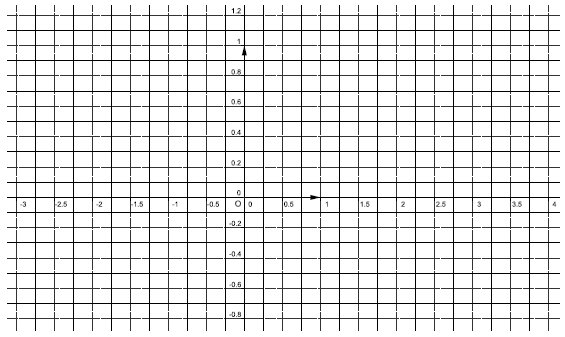
8) Tracer la courbe Cf sur l’intervalle [−3 ; 4] ci-dessous.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, rationnelle, second degré.
Exercice précédent : Second degré – Triangles, forme canonique, inéquations – Première

