Maths : exercice sur fonction exponentielle, première. Calcul de la dérivée, tableau de variation, maximum, graphique, application, valeurs.
Exercice N°340 :
f est la fonction définie sur R par :
f(x) = 50xe-0,5x+1.
Une partie de la courbe représentative Cf de f est donnée ci-dessous.
Le point A est le point de Cf d’abscisse 4 et le point B est le point de Cf d’ordonnée maximale.
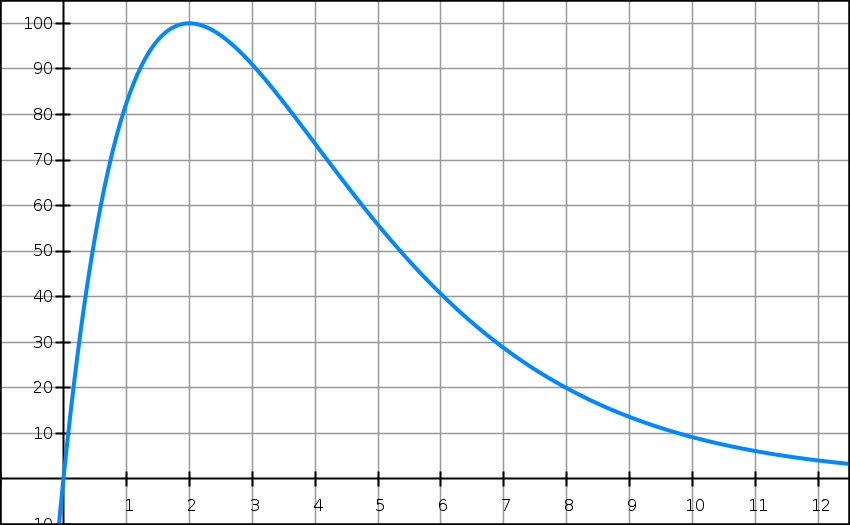
1) Calculer les valeurs de f(0), f(2), f(4) et f(7) arrondies à 10-2 près.
2) Montrer que, pour tout nombre réel x :
f ‘ (x) = (50 – 25x)e-0,5x+1.
3) Construire le tableau de variation de f.
Un laboratoire teste la qualité d’un composant d’une nouvelle crème solaire. Il agit comme un réservoir d’hydratation pour la peau exposée au soleil. Pour cela, on mesure le taux d’hydratation de la peau x heures après l’application.
La fonction f correspond au taux mesuré, exprimé en pourcentage pendant 11 heures.
4) Quelle information le calcul de f(4) effectué en 1) donne-t-il au laboratoire ?
5) Calculer f ‘ (4). Quelle information ce calcul donne-t-il au laboratoire ?
6) Indiquer le moment où le taux est maximal.
7) Déterminer graphiquement les moments ou le taux est égal à 30 %.
8) On peut commercialiser cette crème si le taux d’hydratation dépasse 50 % pendant une durée d’au moins six heures. Le laboratoire peut-il commercialiser cette crème ?
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, fonction exponentielle, première.
Exercice précédent : Exponentielle – Courbe, variations, convexité, bénéfice – Terminale

