Exercice de maths de terminale sur la fonction exponentielle avec calcul de dérivée, factorisation, tableaux de variation, inéquations.
Exercice N°341 :
Exercice N°341 :
On considère la fonction f définie sur R par
f(x) = 2ex – e2x.
1) Calculer la dérivée f ‘ de f. Lis la suite »
Maths de seconde de second degré : exercice sur sommet d’une fonction « parabole ». Extremum, minimum, maximum, tableau de variation.
Exercice N°154 :
Exercice N°154 :
Le prix de vente d’un objet, en euros, est fonction de la demande pour cet objet. On suppose que le prix de vente est donné par
f(x) = 2x2 – 28x + 195
où x est le nombre d’objets demandés et vendus.
1) Y a-t-il une valeur de x pour laquelle le prix de vente est minimal ? maximal ? Lis la suite »
Maths de première : exercice sur fonction rationnelle avec variation. Domaine de définition, expression, quotient, fraction, égalités.
Exercice N°076 :
Soit f la fonction définie par :
f(x) = (2x – 4)/(x + 2)
1) Déterminer le domaine de définition Df de f. Lis la suite »
Exercice de maths de seconde sur domaine de définition avec fonction, fraction rationnelle. Polynôme du second degré, dénominateur, équation.
Exercice N°343 :
Exercice N°343 :
1-2-3-4-5-6-7) Déterminer l’ensemble de définition de chacune des fonctions suivantes :
1) f(x) = (x + 7)/(4x – 12), Lis la suite »
Maths de seconde : exercice de géométrie sur les droites avec intersection. Calculs d’équation, milieu, coordonnées de point d’intersection.
Exercice N°061 :
Dans le plan muni d’un repère orthonormal, on considère les points A(-4 ; 3), B(22/3 ; 5) et C(2 ; 7).
0) Faites la figure au fur et à mesure des questions.
1) Tracer la droite (d) d’équation y = -x + 4 en expliquant la méthode choisie. Lis la suite »
Maths : exercice sur l’exponentielle avec système et variation, valeurs intermédiaires, coût, primitive, intégrale, première, terminale.
Exercice N°335 :
Exercice N°335 :
Soit f la fonction définie sur [0 ; 5] par
f(x) = (ax + b)e−x
où a et b sont deux réels.
On note f ‘ la fonction dérivée de f.
1) Montrer que pour tout nombre réel x,
f ‘ (x) = (a − b − ax)e−x. Lis la suite »
Maths de seconde : exercice avec fonctions, équations, inéquations. Résolutions graphiques et par calcul. Polynôme du second degré et droite.
Exercice N°046 :
0) Démontrer que la fonction h représentée ci-dessus :
x → x2 + 4
est croissante sur [0 ; +∞ [.
On considère le fonctions f et g définies par
f(x) = (1/2) x2
et
g(x) = 3x – 4.
1) Représenter dans un autre et même repère les courbes Cf et Cg des fonctions f et g sur l’intervalle [-4 ; 6]. Lis la suite »
Exercice de maths de terminale sur les primitives et intégrales avec variation et inégalité, tableau de signe, limite, fonction exponentielle.
Exercice N°429 :
On considère une fonction f dérivable sur l’intervalle ]−∞ ; +∞[.
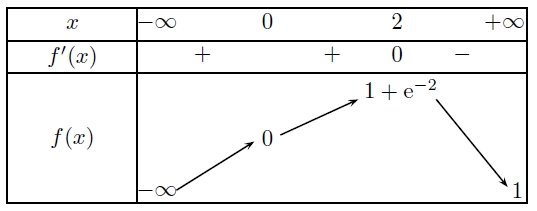
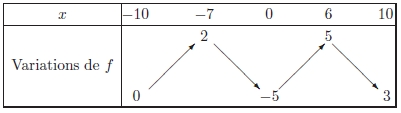
On donne le tableau de ses variations :
Soit g la fonction définie sur ]−∞ ; +∞[ par
g(x) = ∫[de 0 à x] f(t)dt
Partie A :
1) En tenant compte de toutes les informations contenues dans le tableau de variation, tracer une courbe (C) susceptible de représenter f dans le plan muni d’un repère orthogonal (unités graphiques : 1 cm sur l’axe des abscisses, 2 cm
sur l’axe des ordonnées).
2) Interpréter graphiquement g(2). Lis la suite »
Exercice de maths de première de fonction, tableau de variation, définition, équation, polynôme, racine, croissance, encadrement.
Exercice N°320 :
Exercice N°320 :
On donne le tableau de variations d’une fonction f définie
sur [−10; 10].
1) A l’aide du tableau comparer :
f(1) et f(3),
f(−5) et f(−3),
f(7) et f(−2). Lis la suite »
Exercice de maths de première sur domaine de définition avec fonction rationnelle, racine, quotient, rationnelle, inverse, signe, intervalle.
Exercice N°314 :
Exercice N°314 :
1-2-3-4) Donner le domaine de définition de chacune des fonctions suivantes. Le résultat sera donné sous forme d’intervalle ou de réunion d’intervalles. Préciser le raisonnement en détaillant les contraintes à vérifier.
1) f(x) = (3x + 2)/(x² + 2x + 5), Lis la suite »
