Exercice de maths de première de fonction, tableau de variation, définition, équation, polynôme, racine, croissance, encadrement.
Exercice N°320 :

Exercice N°320 :
On donne le tableau de variations d’une fonction f définie
sur [−10; 10].
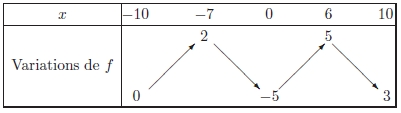
1) A l’aide du tableau comparer :
f(1) et f(3),
f(−5) et f(−3),
f(7) et f(−2).
2) Quel est le minimum de f sur [−10; 10] ? le maximum ?
3) Combien l’équation f(x) = 0 admet-elle de solutions ?
Soit g la fonction définie sur R par
g(x) = 1 − 2x3.
4) Montrer que g est décroissante sur R.
5) A l’aide de la calculatrice, donner une valeur arrondie au dixième de α, solution de l’équation g(x) = 0.
Soit h la fonction définie sur [2 ; +∞[ par
h(x) = 3√(x − 2).
6) Justifier le domaine de définition de la fonction h.
7) Montrer que h est croissante sur [2 ; +∞[.
8) En déduire un encadrement de h(x) pour x compris entre 3 et 6.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : tableau, variation, définition, équation.
Exercice précédent : Fonctions – Images, antécédents, variations, signes – Première


Comment trouves-t-on déjà le minimum et le maximum?
2) Quel est le minimum de f sur [−10; 10] ? le maximum ?
Le minimum est la valeur en ordonnée la plus basse sur le tableau de variation, soit -5.
Le maximum est la valeur en ordonnée la plus haute sur le tableau de variation, soit 5.
Exact, merci !