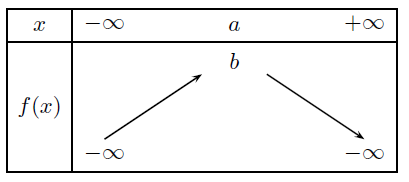
Exercice de maths de terminale sur la limite, l’exponentielle, suite, continuité. Dérivée, tableau de variation, fonction, démonstration.

Exercice N°283 :

Exponentielle, fonctions, suite, continuité, limite, terminale

Soit n un entier naturel.
On note fn la fonction définie sur l’ensemble R des nombres réels par :
fn(x) = e−nx/(1 + e−x).
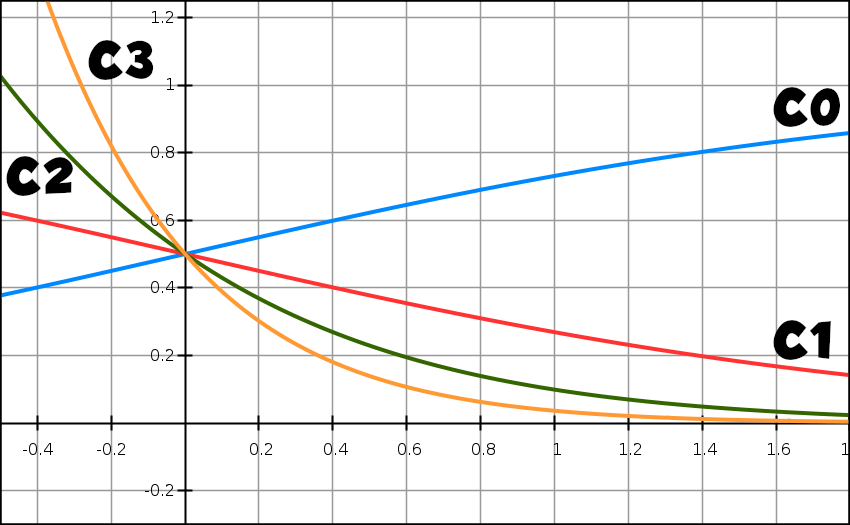
On note Cn la courbe représentative de fn dans un repère orthogonal
(O ; →i ; →j).
Les courbes C0, C1, C2 et C3 sont représentées ci-dessus.

1) Démontrer que pour tout entier naturel n, les courbes Cn ont un point A en commun. On précisera ses coordonnées. Lis la suite »

Ecris le premier commentaire

Exercice de maths de terminale avec fonction, dérivée, limite, tableau de variation, suite, somme géométrique, exponentielle, convergence.

Exercice N°282 :

Exponentielle, fonction, suite, variation, somme, terminale

Exercice N°282 :

On considère la fonction f définie sur l’intervalle ]0 ; +∞[ par :
f(x) = x/(ex−1).

On rappelle que la fonction exponentielle est l’unique fonction g dérivable sur R vérifiant :
{ g ‘ (x) = g(x) pour tout x ∈ R et g(0) = 1.

1) Démontrer que limh→0 (eh − 1)/h = 1. Lis la suite »

Ecris le premier commentaire

Maths : exercice d’exponentielle avec algorithme de terminale. Fonction, variation, limite, équation, tangente, position relative, continuité

Exercice N°279 :

Exercice, exponentielle, algorithme, terminale, fonction, polynôme

On considère la fonction f définie sur R par
f(x) = e−x + x.
On note C sa courbe représentative dans un repère orthonormal.

1) Calculer les limites de f en +∞ et −∞.
Au voisinage de −∞, on pourra démontrer que
f(x) = e−x (1 + xex). Lis la suite »

Ecris le premier commentaire

Maths de terminale: exercice d’exponentielle avec variation, courbe représentative, dérivée, signe, croissance, décroissance, limite.

Exercice N°276 :

Soit f une fonction dérivable sur R dont le tableau de variations est donné ci-contre où a et b désignent deux réels.

Exercice, exponentielle, variation, courbe, tableau

1) Déterminer le signe de f ‘ (x) selon les valeurs de x. Lis la suite »

Ecris le premier commentaire

Maths de terminale : exercice sur la fonction logarithme népérien. Limites, variations, tangentes, polynômes, tangente, équations, courbe.

Exercice N°631 :

Exercice, fonction, logarithme népérien, limites, tangentes, terminale

Exercice N°631 :

Soit f la fonction définie sur ]1 ; +∞[ par :
f(x) = ln(x) – ( 1/ln(x) ).

On note C sa courbe représentative dans un repère orthogonal d’origine O et Γ la courbe représentative de la fonction ln.

1) Étudier les variations de f et ses limites en 1 et +∞. Lis la suite »

Ecris le premier commentaire

Maths : exercice d’exponentielle, domaine de définition. Variation, tangente, première, fraction, dérivée, tableau de signe, équation.

Exercice N°691 :

Exponentielle, définition, variation, équations de tangente, première, La Seine, Paris

Exercice N°691 :

Soit f la fonction définie par :
g(x) = (x + 2)/ex.

1) Justifier que f est définie sur R. Lis la suite »

Ecris le premier commentaire

Maths de première : exercice d’exponentielle avec polynôme, quotient. Dérivée, tableau de signe, tableau de variation, équation. solutions.

Exercice N°690 :

Exercice, exponentielle, polynôme, quotient, dérivée, signe, variation, équation, première

Exercice N°690 :

Soit f la fonction définie sur R par :
f(x) = e2x + 4ex – 6x.

1) Calculer f ‘ (x) et montrer que
f ‘ (x) = 2(ex – 1)(ex + 3). Lis la suite »

Ecris le premier commentaire

Exercice de maths de terminale de logarithme népérien avec primitive et intégrale. Dérivée, variation et convexité, courbe et aire en dessous.

Exercice N°415 :

Logarithme népérien, primitive, intégrale, dérivée, variation, terminale

Soit f la fonction définie pour tout réel x strictement positif par
f(x) = (2ln(x) + 4)/x.

1) Résoudre l’inéquation f(x) ≥ 0. Lis la suite »

Ecris le premier commentaire

     Articles suivants »
✕
FrenchMaths.com

GRATUIT
VOIR