Exercice de maths de première sur une suite récurrente avec termes sur graphique. Fonction, variation, calcul, graphique, droite, tracer.
Exercice N°412 :
Soit (un) la suite définie par u0 = 10 et pour tout entier naturel n,
un+1 = 8 − 0,12 × un2.
1) Calculer u1 et u2.
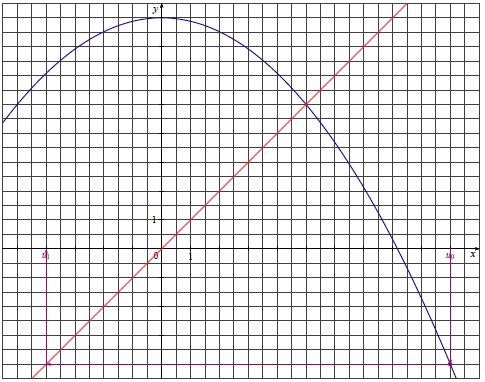
On a tracé ci-dessous dans un repère orthonormé, la courbe représentative de la fonction f définie pour tout réel x
par f(x) = 8 − 0,12x2
et la droite D d’équation y = x.
On a représenté sur l’axe des abscisses du graphique ci-dessus, les deux premiers termes de la suite (un).
2) Construire sur l’axe des abscisses les termes u1, u2, u3 et u4.
3) La suite (un) est-elle monotone ?
Questions indépendantes :
On note (vn) la suite définie de manière récurrente pour tout entier naturel par :
{ v0 = 2,
{ vn+1 = vn + 1/(n+1).
4) Étudier le sens de variation de (vn).
On note (wn) la suite définie de manière récurrente pour tout entier naturel par :
{ w0 = 2,
{ wn+1 = wn – n2.
5) Étudier le sens de variation de (wn).
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : suite récurrente, termes, graphique.
Exercice précédent : Suites – Géométrique, arithmétique, variation, raison – Première

