Maths de première : exercice de géométrie sur angles et triangles. Complémentaires, supplémentaires, points alignés, formules vecteurs.
Exercice N°139 :
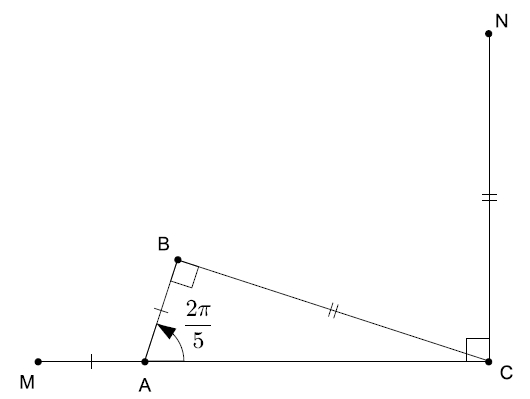
Sur la figure ci-dessus, on sait que l’angle (→AC, →AB) = 2π/5 en radian.
1) Déterminer une mesure exacte de l’angle (→AB, →AM) en radian.
2) En déduire que l’angle (→BM, →BA) = π/5 en radian.
3) Déterminer la valeur exacte de l’angle (→CN, →CB) en radian.
4) En déduire que l’angle (→BC, →BN) = 3π/10 en radian.
5) En déduire que les points M, N et B sont alignés.
Partie indépendante :
6) Donner la valeur exacte de sin(7π/4) en justifiant à l’aide d’un schéma.
7) Donner la valeur exacte de sin(2π/3) en justifiant à l’aide d’un schéma.
8) Donner la valeur exacte de sin(19π/3) en déterminant la valeur principale et en justifiant à l’aide d’un schéma.
9) Donner la valeur exacte de sin(25π/6) en déterminant la valeur principale et en justifiant à l’aide d’un schéma.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, géométrie, angles, triangles.
Exercice précédent : Trigonométrie – Cercle d’Euler et mesures principales – Première

