Exercice de maths : intégrales, primitives, limites de terminale. Fonction, aire, exponentielle, position relative, équation, suite, courbe.
Exercice N°462 :
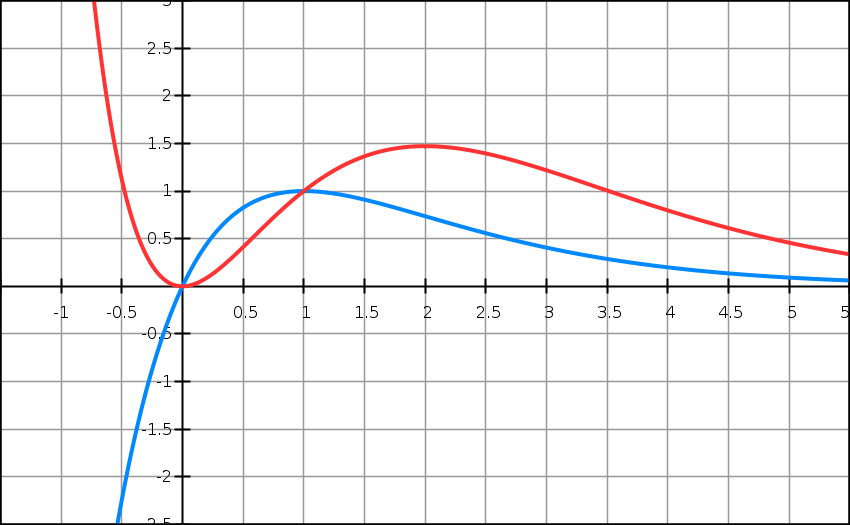
Soient f et g les fonctions définies sur l’ensemble R des nombres réels par
f(x)= xe1−x
et
g(x) = x2e1−x.
Les courbes représentatives des fonctions f et g dans un repère orthogonal
(0 ; →i : →j) sont respectivement notées C et C ‘. Leur tracé est donné ci-dessus.
Étude des fonctions f et g :
1) Déterminer les limites des fonctions f et g en -∞.
2) Déterminer la limite de la fonction f en +∞. On admettra que la fonction g a pour limite 0 en +∞.
3) Étudier le sens de variations de chacune des fonctions f et g et dresser leurs tableaux de variations respectifs.
Calcul d’intégrales :
Pour tout entier naturel n , on définit l’intégrale In par :
I0 = ∫[de 0 à 1] e1−x dx
et, pour n ⩾ 1,
In = ∫[de 0 à 1] xne1−x dx.
4) Calculer la valeur exacte de I0.
5) Déterminer pour n ≥ 0, la dérivée de la fonction h définie sur R par
h(x) = xn+1e1−x.
En déduire que pour tout entier naturel n ≥ 0 :
In+1 = −1 + (n+1)In.
6) En déduire la valeur exacte de I1, puis celle de I2.
Calcul d’une aire plane :
7) Étudier la position relative des courbes C et C ‘.
On désigne par A l’aire, exprimée en unité d’aire, de la partie du plan comprise d’une part entre les courbes C et C ‘, d’autre part entre les droites d’équations respectives x = 0 et x = 1.
8) En exprimant A comme différence de deux aires que l’on précisera, démontrer l’égalité :
A = 3 − e.
Étude de l’égalité de deux aires :
Soit a un réel strictement supérieur à 1.
On désigne par S(a) l’aire, exprimée en unité d’aire, de la partie du plan comprise d’une part entre les courbes C et C ‘, d’autre part entre les droites d’équations respectives x = 1 et x = a.
L’objectif de cette question est de prouver qu’il existe une et une seule valeur de a pour laquelle les aires A et S(a) sont égales.
9) Montrer que S(a)= 3 − e1−a(a2 + a + 1) à l’aide des résultats donnés ci-dessous par un logiciel de calcul formel :

10) Démontrer que l’équation S(a) = A est équivalente à l’équation :
ea = a2 + a + 1.
Question “toute trace de recherche” :
11) Conclure, quant à l’existence et l’unicité du réel a, solution du problème posé.
Bon courage,
Sylvain Jeuland
Pour avoir la suite du corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels du second degré (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés de l’exercice : intégrales, limites, primitives, terminale.
Exercice précédent : Primitives – ROC, logarithme, fractions, intégrale – Terminale

