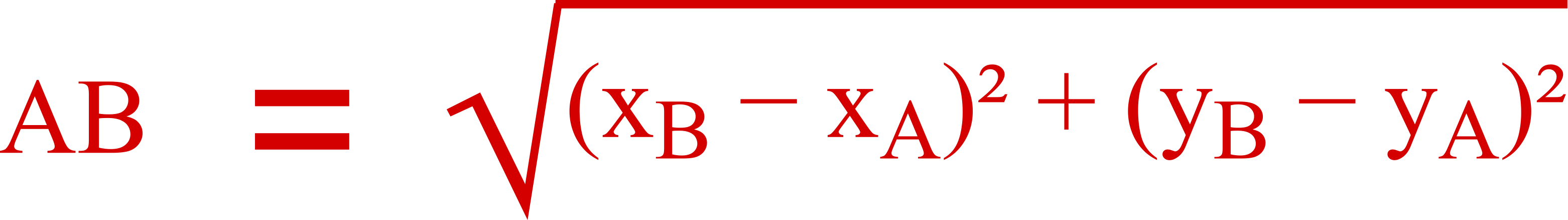frenchmaths.com (par Sylvain Jeuland)

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) On a ^→AG = ²/₃^→AB.

Montrons que ¹/₃^→GA + ²/₃^→GB = ^→0 :

On part de la gauche pour espérer tomber sur le vecteur nul.

¹/₃^→GA + ²/₃^→GB
= ¹/₃(-^→AG) + ²/₃(^→GA + ^→AB)
= ¹/₃(-^→AG) + ²/₃(-^→AG + ^→AB)
= –¹/₃^→AG – ²/₃^→AG + ²/₃^→AB
= –^→AG + ²/₃^→AB
= –²/₃^→AB + ²/₃^→AB
= ^→0.

2) On a -5^→HA + 6^→HB + 9^→HC = ^→0.

Montrons que ^→AH = ³/₅^→AB + ⁹/₁₀^→AC :

-5^→HA + 6^→HB + 9^→HC = ^→0
⇔ -5^→HA + 6(^→HA + ^→AB) + 9(^→HA + ^→AC) = ^→0
⇔ -5^→HA + 6^→HA + 6^→AB + 9^→HA + 9^→AC = ^→0
⇔ 10^→HA + 6^→AB + 9^→AC = ^→0
⇔ -10^→AH + 6^→AB + 9^→AC = ^→0
⇔ 6^→AB + 9^→AC = 10^→AH
⇔ 10^→AH = 6^→AB + 9^→AC
⇔ ^→AH = ⁶/₁₀^→AB + ⁹/₁₀^→AC
⇔ ^→AH = ³/₅^→AB + ⁹/₁₀^→AC

3) On a ^→KA + 3^→KC = ^→0.

Exprimons ^→AK en fonction de ^→AC :

^→KA + 3^→KC = ^→0
⇔ ^→KA + 3^→KC = ^→0
⇔ ^→;KA + 3(^→KA + ^→AC) = ^→0
⇔ ^→KA + 3^→KA + 3^→AC = ^→0
⇔ 4^→KA + 3^→AC = ^→0
⇔ -4^→AK + 3^→AC = ^→0
⇔ 3^→AC = 4^→AK
⇔ ³/₄^→AC = ^→AK
⇔ ^→AK = ³/₄^→AC

4) On a ^→LA + 2^→LB + 3^→LC = ^→0.

Montrons que ^→AL = ¹/₃^→AB + ¹/₂^→AC :

^→LA + 2^→LB + 3^→LC = ^→0
⇔ ^→LA + 2(^→LA + ^→AB) + 3(^→LA + ^→AC) = ^→0
⇔ ^→LA + 2^→LA + 2^→AB + 3^→LA + 3^→AC = ^→0
⇔ 6^→LA + 2^→AB + 3^→AC = ^→0
⇔ -6^→AL + 2^→AB + 3^→AC = ^→0
⇔ 2^→AB + 3^→AC = 6^→AL
⇔ 6^→AL = 2^→AB + 3^→AC
⇔ ^→AL = ²/₆^→AB + ³/₆^→AC
⇔ ^→AL = ¹/₃^→AB + ¹/₂^→AC

5) Montrons que L milieu de [GC] :

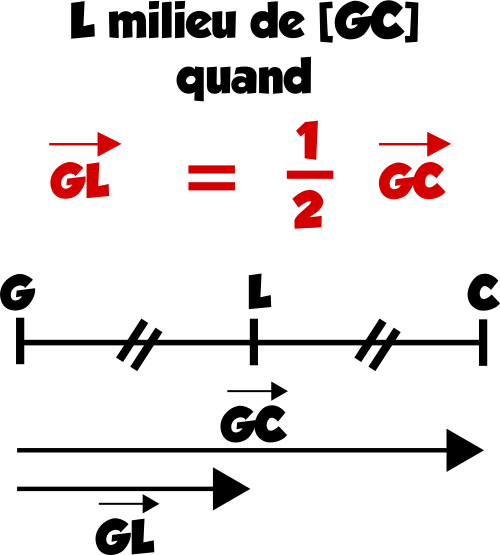
L’idée est d’exprimer les vecteurs ^→GL (à gauche) et ¹/₂^→GC (à droite) en fonction des vecteurs non colinéaires ^→AB et ^→AC.

D’une part, ^→GL = ^→GA + ^→AL
= –^→AG + ^→AL
= –²/₃^→AB + ¹/₃^→AB + ¹/₂^→AC
= –¹/₃^→AB + ¹/₂^→AC

D’autre part, ¹/₂^→GC
= ¹/₂(^→GA + ^→AC)
= ¹/₂^→GA + ¹/₂^→AC
= ¹/₂^→GA + ¹/₂^→AC
= ¹/₂(-^→AG) + ¹/₂^→AC
= ¹/₂(-^→AG) + ¹/₂^→AC
= ¹/₂(-²/₃^→AB) + ¹/₂^→AC
= –¹/₃^→AB + ¹/₂^→AC

Les coefficients devant ^-→AB et ^→AC sont les même donc on a bien ^→GL = ¹/₂^→GC.

Du coup, L est bien le milieu de [GC].

6) Montrons que L, A, H alignés :

L, A et H sont alignés si et seulement si les vecteurs ^->AL et ^→AH sont colinéaires.
Ils sont colinéaires si et seulement si leurs coordonnées x et x’, puis y et y’ sont proportionnelles.

Comme ces vecteurs sont exprimés en fonction des vecteurs non colinéaires ^→AB et ^→AC, on peut utiliser le repère (A ; ^→AB ; ^→AC). Les coordonnées x et y, puis x’ et y’ sont les coefficients devant ces vecteurs.

D’une part, ^→AL = ¹/₃^→AB + ¹/₂^→AC.

Donc x = ¹/₃ et y = ¹/₂.

D’autre part, ^→AH = ³/₅^→AB + ⁹/₁₀^→AC.

Donc x’ = ³/₅ et y’ = ⁹/₁₀.

On a donc le tableau :
¹/₃ | ¹/₂
³/₅ | ⁹/₁₀

Les produits en croix sont :
¹/₃ × ⁹/₁₀
= ⁹/₃₀ = ³/₁₀
Et :
³/₅ × ¹/₂
= ³/₁₀.

Donc les produits en croix sont égaux, x’y – xy’ = 0, les coordonnées sont proportionnelles, donc les vecteurs ^→AL et ^→AH sont colinéaires et les points A, L et H sont alignés.

7) Montrons que L ∈ (KB) :

L ∈ (KB)
si et seulement si,
L, K et B sont alignés.

La lettre K se trouve dans la formule ^→AK = ³/₄^->AC donc insérons un A dans ^->BK avec la relation de Chasles.
Comme on a aussi ^->AL, insérons un A dans ^→BL.

L, K et B sont alignés si et seulement si ^→BK et ^→BL sont colinéaires. Regardons si leurs coordonnées dans le repère (A ; ^→AB ; ^→AC) sont proportionnelles.

D’une part, ^→BK = ^→BA + ^→AK
= -1^→AB + ³/₄^→AC.
Les coordonnées x et y sont -1 et ³/₄.

D’autre part, ^→BL = ^→BA + ^→AL
= -1^→AB + ¹/₃^→AB + ¹/₂^→AC
= –²/₃^→AB + ¹/₂^→AC.
Les coordonnées x’ et y’ sont –²/₃ et ¹/₂.

Le tableau est :
-1 ; ³/₄
–²/₃ ; ¹/₂

Les produits en croix sont :
-1 × ¹/₂
= –¹/₂
Et :
³/₄ × –²/₃
= –¹/₂.

Donc les produits en croix sont égaux, x’y – xy’ = 0, les coordonnées sont proportionnelles, donc les vecteurs ^→BK et ^→BL sont colinéaires et les points B, K et L sont alignés. Du coup, L appartient à (KB).

8) Que peut-on dire des droites (GC), (HA) et (KB) :

L appartient à (GC), à (HA) et à (KB) donc les trois droites se coupent en un même point L. Elles sont concourantes.

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Expressions de f₁(x), f₂(x) et f₃(x) :

Ce sont les dépenses des forfaits 1, 2 et 3 en fonction du nombre de minutes hors-forfait qui vaut x. Ils correspondent au y dans les équations de droites :
y₁, y₂ et y₃.

Le « bon sens de la vie courante » à propos des forfaits téléphoniques dit que le prix payé est fixe pour 2h de communication et qu’on additionne un coût par minute de communication supplémentaire hors-forfait.

Pour le forfait 1 d’après le tableau :
2h de forfait fixe : 30 euros,
1 minute supplémentaire : 0,25 euros.
Donc x minutes supplémentaires valent 0.25x euros.
Quand on additionne le prix fixe des 2h et les x minutes supplémentaires, cela donne la dépense du forfait 1,
f₁(x) = 30 + 0,25x = 0,25x + 30.

Pour le forfait 2 d’après le tableau :
2h de forfait fixe : 15 euros,
1 minute supplémentaire : 0,75 euros.
Donc x minutes supplémentaires valent 0.75x euros.
Quand on additionne le prix fixe des 2h et les x minutes supplémentaires, cela donne la dépense du forfait 2,
f₂(x) = 15 + 0,75x = 0,75x + 15.

Pour le forfait 3 d’après le tableau :
2h de forfait fixe : 20 euros,
1 minute supplémentaire : 0,5 euros.
Donc x minutes supplémentaires valent 0.5x euros.
Quand on additionne le prix fixe des 2h et les x minutes supplémentaires, cela donne la dépense du forfait 1,
f₃(x) = 20 + 0,5x = 0,5x + 20.

2) Résoudre les équations :

On résout :
f₁(x) = f₂(x)
⇔ 0,25x + 30 = 0,75x + 15
⇔ 0,25x + 30 – 0,75x – 30 = 0,75x + 15 – 0,75x – 30
⇔ -0,50x = -15
⇔ x = (-15)/(-0,50)
⇔ x = 30.

On résout :
f₂(x) = f₃(x)
⇔ 0,75x + 15 = 0,5x + 20
⇔ 0,75x + 15 – 0,5x – 15 = 0,5x + 20 – 0,5x – 15
⇔ 0.25x = 5
⇔ x = 5/0.25
⇔ x = 20.

On résout :
f₁(x) = f₃(x).
⇔ 0,25x + 30 = 0,5x + 20
⇔ 0,25x + 30 – 0,5x – 30 = 0,5x + 20 – 0,5x – 30
⇔ -0,25x = -10
⇔ x = (-10)/(-0,25)
⇔ x = 40.

3) Tracer les droites :

La technique idéale pour tracer une droite sur un graphique est de placer deux points appartenant à la droite et de tracer la droite passant par ces deux points. Pour ce faire, il faut choisir pour chaque point l’abscisse que l’on veut puis calculer l’ordonnée avec l’équation de cette droite.

Pour la droite représentant le forfait 1, on prend l’équation
y = f₁(x) = 0,25x + 30 et on choisit l’abscisse x = 60. L’ordonnée y correspondante vaut y = 0,25×60 + 30 = 15 + 30 = 45. Le point A(60 ; 45) est donc sur cette droite.

On peut prendre comme abscisse du second point x = 20, ce qui donne
y = 0.25×20 + 30 = 5 + 30 = 35. Ce point a pour coordonnées B(20 ; 35). On peut maintenant tracer la droite.

On vérifie que la droite passe par l’ordonnée à l’origine 30 soit le point (0 ; 30).

Pour la droite représentant le forfait 2, on prend l’équation
y = f₂(x) = 0,75x + 15 et on choisit l’abscisse x = 60. L’ordonnée y correspondante vaut y = 0,75×60 + 15 = 45 + 15 = 60. Le point E(60 ; 60) est donc sur cette droite.

On peut prendre comme abscisse du second point x = 20, ce qui donne
y = 0.75×20 + 15 = 15 + 15 = 30. Ce point a pour coordonnées F(20 ; 30). On peut maintenant tracer la droite.

On vérifie que la droite passe par l’ordonnée à l’origine 30 soit le point (0 ; 15).

Pour la droite représentant le forfait 3, on prend l’équation
y = f₃(x) = 0,5x + 20 et on choisit l’abscisse x = 60. L’ordonnée y correspondante vaut y = 0,5×60 + 20 = 30 + 20 = 50. Le point G(60 ; 50) est donc sur cette droite.

On peut prendre comme abscisse du second point x = 20, ce qui donne
y = 0.5×20 + 20 = 10 + 20 = 30. Ce point a pour coordonnées H(20 ; 30). On peut maintenant tracer la droite.

On vérifie que la droite passe par l’ordonnée à l’origine 20 soit le point (0 ; 20).

Voici les droites tracées :

4) La courbe g représente le tarif le plus avantageux quelque soit le nombre de minutes hors forfait. Le tarif le plus avantageux est le tarif le « moins cher » qui est représenté par la droite la plus basse pour un nombre de minutes donnée.

Il faut donc partir de la gauche avec un crayon rouge et suivre jusqu’au bout les droites les plus basses. On doit changer de droites pour pouvoir représenter la fonction g car le tarif le plus bas change en fonction du nombre de minutes.

Oui une fonction n’est pas toujours définie par une seule expression mathématique. Ici l’expression de g(x) est définie par le minimum de f₁(x), f₂(x) et f₃(x) selon les valeurs de x. Donc la courbe Cg est l’ensemble des segments de droites les plus bas.

Voici la courbe Cg en fluo rose :

5) Pour ajouter 25 minutes et choisir la bonne formule, il faut partir de l’abscisse x = 25 sur l’axe des abscisses. Puis il faut remonter verticalement jusqu’à la courbe Cg. Voici la droite choisie en vert :

On voit sur la courbe ci-dessus que pour l’abscisse x = 25, nous arrivons en Cg sur la portion de droite D₃ qui réprensente la formule N°3. Cette personne doit donc choisir cette formule.

Bonne compréhension,
laisse un commentaire pour toute question ou incompréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Lorsque le premier locataire arrive, le concierge peut donner 3 clés différentes à celui-ci.

Ensuite, le deuxième locataire arrive et le concierge peut lui remettre l’une 2 clés différentes restantes.

Enfin, le dernier arrive et il prend la dernière clé restante.
Cela fait donc 3×2×1 possibilités en tout. Donc le concierge a 6 façons de remettre les clés aux locataires.

2) Si deux locataires retrouvent leur clé respective, forcément le 3ème aura sa clé aussi. Donc il n’est possible d’avoir seulement deux locataires qui ont retrouvé leur clé.

3) Pas facile sans un arbre, en voici un avec les locataires qui arrivent dans l’ordre et qui reçoivent leur clé.

J’ai entouré les mots « Clé » quand le locataire reçoit sa propre clé et à droite j’ai entouré le nombre de clés bien rendues.

F – « Les trois locataires retrouvent leur clé. »

Un seul chemin donc (¹/₃)×(¹/₂) = ¹/₆.

G – « Un seul des trois locataires reçoive sa clé. »

On voit qu’il y a trois chemins correspondants donc 3×(¹/₆) = ¹/₂.

H : « Aucun des locataires ne retrouve sa clé ».

On voit qu’il y a deux chemins correspondants donc 2×(¹/₆) = ¹/₃.

On vérifie bien que
¹/₆ + ¹/₂ + ¹/₃
= ¹/₆ + ³/₆ + ²/₆
= ⁶/₆
= 1
pour couvrir tous les cas.
On garde en mémoire que rendre correctement 2 clés n’est pas possible.

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Pour calculer la mesure d’un principale d’un angle, l’idéal est de mettre 2π sous la forme d’une fraction avec le même dénominateur que notre angle.
2π = ^6π/₃

La mesure principale doit se situer dans l’intervalle ]-π ; π]. Là aussi, l’idéal est de mette les π sous la forme d’une fraction avec le même dénominateur que notre angle.
]-π ; π] = ]-^3π/₃ ; ^3π/₃].

Si l’angle de départ est au delà de l’intervalle ]-π ; π], il faut enlever les 2π jusqu’à l’atteindre.
Si l’angle de départ est en deçà de l’intervalle ]-π ; π], il faut ajouter les 2π jusqu’à l’atteindre.

Du coup, comme j’ai tout mis sur le même dénominateur et qu’il y a des π partout, on peut partir de 13 (pour ^13Π/₃), enlever plusieurs fois 6 (pour ^6π/₃) pour arriver dans l’intervalle ]-3 ; 3] (pour ]-^3π/₃ ; ^3π/₃]).

13 – 6 = 7
7 – 6 = 1
1 appartient bien à ]-3 ; 3] donc la mesure principale est ^1Π/₃.

2) Pour calculer la mesure d’un principale d’un angle, l’idéal est de mettre 2π sous la forme d’une fraction avec le même dénominateur que notre angle.
2π = ^10π/₅

La mesure principale doit se situer dans l’intervalle ]-π ; π]. Là aussi, l’idéal est de mette les π sous la forme d’une fraction avec le même dénominateur que notre angle.
]-π ; π] = ]-^5π/₅ ; ^5π/₅].

Si l’angle de départ est au delà de l’intervalle ]-π ; π], il faut enlever les 2π jusqu’à l’atteindre.
Si l’angle de départ est en deçà de l’intervalle ]-π ; π], il faut ajouter les 2π jusqu’à l’atteindre.

Du coup, comme j’ai tout mis sur le même dénominateur et qu’il y a des π partout, on peut partir de 18 (pour ^18Π/₅), ajouter soustraire plusieurs fois 10 (pour ^10π/₅) pour arriver dans l’intervalle ]-5 ; 5] (pour ]-^5π/₅ ; ^5π/₅]).

18 – 10 = 8
8 – 10 = -2
-2 appartient bien à ]-5 ; 5] donc la mesure principale est ^-2Π/₃.

3) Pour calculer la mesure d’un principale d’un angle, l’idéal est de mettre 2π sous la forme d’une fraction avec le même dénominateur que notre angle.
2π = ^14π/₇

La mesure principale doit se situer dans l’intervalle ]-π ; π]. Là aussi, l’idéal est de mette les π sous la forme d’une fraction avec le même dénominateur que notre angle.
]-π ; π] = ]-^7π/₇ ; ^7π/₇].

Si l’angle de départ est au delà de l’intervalle ]-π ; π], il faut enlever les 2π jusqu’à l’atteindre.
Si l’angle de départ est en deçà de l’intervalle ]-π ; π], il faut ajouter les 2π jusqu’à l’atteindre.

Du coup, comme j’ai tout mis sur le même dénominateur et qu’il y a des π partout, on peut partir de -24 (pour ^-24Π/₇), ajouter plusieurs fois 14 (pour ^14π/₇) pour arriver dans l’intervalle ]-7 ; 7] (pour ]-^7π/₇ ; ^7π/₇]).

-24 + 14 = -10
-10 + 14 = 4
4 appartient bien à ]-7 ; 7] donc la mesure principale est ^4Π/₇.

4) Pour calculer la mesure d’un principale d’un angle, l’idéal est de mettre 2π sous la forme d’une fraction avec le même dénominateur que notre angle.
2π = ^32π/₁₆

La mesure principale doit se situer dans l’intervalle ]-π ; π]. Là aussi, l’idéal est de mette les π sous la forme d’une fraction avec le même dénominateur que notre angle.
]-π ; π] = ]-^16π/₁₆ ; ^16π/₁₆].

Si l’angle de départ est au delà de l’intervalle ]-π ; π], il faut enlever les 2π jusqu’à l’atteindre.
Si l’angle de départ est en deçà de l’intervalle ]-π ; π], il faut ajouter les 2π jusqu’à l’atteindre.

Du coup, comme j’ai tout mis sur le même dénominateur et qu’il y a des π partout, on peut partir de 1024 (pour ^1024Π/₁₆), enlever plusieurs fois 32 (pour ^32π/₁₆) pour arriver dans l’intervalle ]-16 ; 16] (pour ]-^16π/₁₆ ; ^16π/₁₆]).

1024 – 32 = 992
992 – 32 = 960
960 – 320 = 640 (j’enlève 10 fois 32)
640 – 320 = 320 (j’enlève 10 fois 32)
320 – 320 = 0 (j’enlève 10 fois 32)

0 appartient bien à ]-16 ; 16] donc la mesure principale est ^0Π/₁₆ = 0.

5) Pour déterminer les placements des angles ^4Π/₃, ^3Π/₄ et ^Π/₆, il faut penser à des gâteaux.
Un gâteau avec des parts de ^Π/₃ est un gâteau avec un découpage pour 6 personnes.
Un gâteau avec des parts de ^Π/₄ est un gâteau avec un découpage pour 8 personnes.
Un gâteau avec des parts de ^Π/₆ est un gâteau avec un découpage pour 12 personnes.

Déjà, détermine la taille d’une part à partir de la gauche (l’angle 0), puis ajoute le nombre de parts de même taille pour arriver au bon angle.
Pour ^4Π/₃, vas jusqu’à 4 parts d’un gâteau de 6 personnes.
Pour ^3Π/₄, vas jusqu’à 3 parts d’un gâteau de 8 personnes.

6) Pour additionner des angles, mets ceux-ci sur le même dénominateur (ici 12).

Α = ^4Π/₃ + ^3Π/₄ + ^Π/₆
= ^16Π/₁₂ + ^9Π/₁₂ + ^2Π/₁₂
= ^{( 16Π + 9Π + 2Π )}/₁₂
= ^27Π/₁₂
= ^3Π/₁₂ (en enlevant 2π)
= ^Π/₄.

Β = ^3Π/₄ – ^Π/₆ – ^4Π/₃
= ^9Π/₁₂ – ^2Π/₁₂ – ^16Π/₁₂
= ^{( 9Π – 2Π – 16Π )}/₁₂
= ^-9Π/₁₂
= ^-3Π/₄.

Γ = ^Π/₆ – ^4Π/₃ – ^3Π/₄.
= ^2Π/₁₂ – ^16Π/₁₂ – ^9Π/₁₂
= ^{( 2Π – 16Π – 9Π )}/₁₂
= ^-23Π/₁₂
= ^Π/₁₂ (en ajoutant 2π).

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Pour démontrer que ABDC est un parallélogramme, il suffit de démontrer que ^→AB = ^→CD.
Les deux dernières lettres sont inversées !

^→AB
{
x_^→AB = x_B – x_A = 3 – (-2) = 5 ;
y_^→AB = y_B – y_A = 3 – 4 = -1.

^→CD
{
x_^→CD = x_D – x_C = 4 – (-1) = 5 ;
y_^→CD = y_D – y_C = -1 – 0 = -1.

Les coordonnées des vecteurs AB et CD sont les mêmes donc ^→AB = ^→CD.
Donc ABDC est un parallélogramme.

2) Si un parallélogramme a deux côtés consécutifs de même longueur, alors c’est un losange.
Calculons donc AB et BD séparément (qui sont deux côtés consécutifs dans le parallélogramme).
Pour ça, on utilise la formule de la distance :

On a déjà calculé x_B – x_A et y_B – y_A au dessus :

AB = √( 5² + (-1)² )
= √26.

BD = √( (x_D – x_B)² + (y_D – y_B)² )
= √( (4 – 3)² + ((-1) – 3)² )
= √( 1² + (-4)² )
= √17.

AB différent de BD donc les côtés consécutifs ne sont pas égaux, donc ABDC n’est pas un losange.

3) On veut que GHKL soit un parallélogramme donc ^→GH doit être égal à ^→LK.
Cette égalité vectorielle équivaut à un système de coordonnées de vecteurs.

{
x_^→GH = x_^→LK,
y_^→GH = y_^→LK
⇔
{
x_H – x_G = x_K – x_L (d’après le cours),
y_H – y_G = y_K – y_L
⇔
{
2 – 0 = -2 – x_L,
1 – 0 = 3 – x_L
⇔
{
2 + 2 = – x_L
1 – 3 = – y_L
(en isolant les coordonnées de L à droite)
⇔
{
x_L = -4
y_L = 2
(en multipliant par -1)

4) Pour démontrer que ^→GE = ^→FK, on calcule les coordonnées de ces vecteurs séparément.

x_^→GE = x_E – x_G = -3 – 0 = -3
y_^→GE = y_E – y_G = -2 – 0 = -2
x_^→FK = x_K – x_F = -2 – 1 = -3
y_^→FK = y_K – y_F = 3 – 5 = -2

On obtient
x_^→GE = x_^→FK,
y_^→GE = y_^→FK.

Les deux vecteurs ont même coordonnées donc ils sont égaux.
Du coup, GEKF est un parallélogramme.

5) Pour montrer que [FE] et [HL] ont même milieu, utilisons la formule des coordonnées d’un milieu sur les deux segments.

Milieu de [FE] :
^{(x_F + x_E)}/₂ = ^{(1 + (-3))}/₂ = ^(-2)/₂ = -1,
^{(y_F + y_E)}/₂ = ^{(5 + (-2))}/₂ = ³/₂.

Milieu de [HL] :
^{(x_H + x_L)}/₂ = ^{(2 + (-4))}/₂ = ^(-2)/₂ = -1,
^{(y_H + yL)}/₂ = ^{(1 + 2)}/₂ = ³/₂.

Les deux milieux ont les mêmes coordonnées, donc c’est le même milieu pour les deux segments.

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé

1) Une hausse de 26% correspond à un coefficient de
(1 + ^p/₁₀₀) = (1 + ²⁶/₁₀₀) = 1,26.

2) Une baisse de 31% correspond à un coefficient de
(1 – ^p/₁₀₀) = (1 – ³¹/₁₀₀) = 0,69.

3) Une baisse de 13% suivie d’une hausse de 17% correspond au produit des coefficients multiplicateurs suivants :
(1 – ^p/₁₀₀) × (1 + ^p/₁₀₀)
= (1 – ¹³/₁₀₀) × (1 + ¹⁷/₁₀₀)
= 0,87 × 1,17
= 1.0179.

4) Multiplier par 1,17 revient à un coefficient multiplicateur supérieur à 1 soit une augmentation.

Pour retrouver le pourcentage, on fait -1 puis ×100. :
1,17 – 1 = 0,17
0,17 × 100 = 17%
soit une hausse de 17%.

5) Multiplier par 0,78 revient à un coefficient multiplicateur inférieur à 1 soit une diminution.

Pour retrouver le pourcentage, on fait -1 puis ×100 :
0,78 – 1 = -0,22
-0,22 × 100 = -22%
soit une baisse de 22%.

6) Diviser par 1,4 revient à calculer le coefficient multiplicateur
¹/_1.4 = 0,7143 environ.

Pour retrouver le pourcentage, on fait -1 puis ×100 :
0,7143 – 1 = -0,1857
-0,1857 × 100 = -18.57%
soit une baisse de 18.57%.

7) Une remise de 20% correspond à une multiplication par le coefficient multiplicateur (1 – ²⁰/₁₀₀) = 0,80.
Une remise de 30% correspond à une multiplication par le coefficient multiplicateur (1 – ³⁰/₁₀₀) = 0,70.

Pour avoir la remise globale qui englobe les deux remises successives, on multiplie les coefficients multiplicateurs 0.80 × 0,70 = 0,56.

Pour retrouver le pourcentage, on fait -1 puis ×100 :
0,56 – 1 = -0,44
-0,44 × 100 = -44.

Le pourcentage de remise globale est de 44%.

8) Si le commerçant augmente ses prix de 15%, cela fait une multiplication de (1 + ¹⁵/₁₀₀) = 1,15.
Il veut solder pour retrouver un prix initial. Pour revenir au prix initial, le second coefficient multiplicateur devra être égal à ¹/_1.15 = 0.86956.

Pour retrouver le pourcentage, on fait -1 puis ×100 :
0,86956 – 1 = -0,13043
-0,13043 × 100 = -13,043

Le pourcentage de baisse sera au maximum de 13.043%.

9) S’il y a 40% de gens qui ont une mauvaise vue, c’est qu’il y a
100-40 = 60% de gens qui ont une bonne vue.

D’après les données, cela fait 45 personnes.

On a donc une ligne avec un pourcentage de 60% et un nombre de 45. Pour avoir le total, il faut placer 100% dans le même tableau et faire le produit en croix :

60% | 45
100% | x

x = 100×45/60 = 75 personnes en tout.

10) 70% des gens qui ont une mauvaise vue, cela correspond à
70/100 FOIS ce nombre de personnes. Ce nombre est donc égal à
0,7×40 = 28 personnes.

Pour connaître le pourcentage par rapport aux 75 personnes du groupe :
28 | 75%
x | 100%

x = 28 × 100/75 = 37,3%.

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Pour avoir le coût marginal C_m(x), on fait la fonction dérivée du coût total
C_T(x) = 2x² + xe^{-2x + 3}.

C_T(x) = 2x² + u(x) × v(x)
avec u(x) = x,
donc u ‘ (x) = 1,
avec v(x) = e^{-2x + 3},
donc v ‘ (x) = -2 × e^{-2x + 3} avec la dérivée de l’exponentielle :

Donc C ‘ _T(x) = 2 × 2x + (u ‘ (x) × v(x) + u(x) × v ‘ (x))
= 4x + 1 × e^{-2x + 3} + x × (-2 × e^{-2x + 3})
On obtient en factorisant par l’exponentielle :
C_m(x) = 4x + (1 – 2x) × e^{-2x + 3}

2) Pour calculer le coût marginal pour 150 articles, on fait :
C_m(1.5) = 4 × 1.5 + (1 – 2 × 1.5) × e^{-2 × 1.5 + 3}
= 6 – 2 × e^{-2 × 1.5 + 3}
= 6 – 2 × e⁰
= 6 – 2 × 1
= 4 milliers d’euros.

C_M(x) = ^C_T(x)/_x
3) Expression de C_M(x) :

C_M(x) = ^{(2x2 + xe-2x + 3)}/_x
= ^{(x × [2x + e-2x + 3])}/_x
(en factorisant par x au numérateur)
= 2x + e^{-2x + 3}
(en simplifiant ^x/_x = 1).

4) Déterminer C_M ‘ (x) :

C_M(x) = 2x + e^{-2x + 3}
On utilise à nouveau la formule de la dérivée de l’exponentielle vue au-dessus.
C_M ‘ (x) = 2 + (-2) × e^{-2x + 3}
= 2 – 2e^{-2x + 3}
= 2 × (1 – e^{-2x + 3})
(comme je vois 2 et 2 dans chaque terme, je factorise par 2)

5) Résolvons l’équation 1 – e^{-2x + 3} = 0 :

1 – e^{-2x + 3} = 0
⇔ 1 = e^{-2x + 3}
⇔ e⁰ = e^{-2x + 3}
⇔ 0 = -2x + 3
⇔ 2x = 3
⇔ x = ³/₂

S = {³/₂}

6) Résolvons l’équation 1 – e^{-2x + 3} > 0 :

1 – e^{-2x + 3} > 0 (expression positive)
⇔ 1 > e^{-2x + 3}
⇔ e⁰ > e^{-2x + 3}
⇔ 0 > -2x + 3
(car exp est strictement croissante, on ne change pas le sens de l’inégalité)
⇔ 2x > 3
⇔ x > ³/₂
(x à droite de ³/₂)

S = ]³/₂ ; +∞[

7) Pour obtenir les variations de C_M, il nous faut le signe de C_M ‘ (x) qui est un produit. On fait le tableau suivant :

8) D’après le tableau de variation de C_M, on voit que le coût moyen est minimal pour une quantité de 1.5 centaine d’articles.

Donc C_M(1.5) = 2 × 1.5 + e^{-2 × 1.5 + 3}
= 3 + e⁰
= 3 + 1 = 4.

Le coût moyen minimal est de 4 milliers d’euros.

R(x) = 7x,
B(x) = R(x) − C_T(x).
Par lecture graphique déterminer :

9) Le coût marginal est décroissant, soit C_m décroissante. Or C_m est la dérivée de C_T donc cela équivaut à C ‘ _T décroissante.
Or C ‘ _T décroissante
⇔ C ‘ ‘ _T(x) négatif
⇔ C_T concave
⇔ C’est quand les tangentes à la courbe sont au-dessus de cette même courbe, c’est-à-dire avant le point d’inflexion de la courbe qui est proche du point d’abscisse 0.7.
L’intervalle de rendement marginal croissant est de [0 ; 0.7].

10) Le coût moyen minimal est atteint en x = 1.5, donc on regarde le coût total qui vaut 6.
Pour obtenir ce coût moyen, on peut rediviser ce coût total par la quantité.
⁶/_1.5 = 4.
On retrouve le coût moyen calculé plus haut.

11) Le bénéfice est positif quand la recette est supérieure au coût. Il faut déterminer les abscisses des points des courbes quand la droite des recettes est au-dessus de la droite du coût.
On remarque que le bénéfice est positif pour des quantités allant de 0.6 à 3.5 centaines d’articles.

12) Pour obtenir la quantité x₀ avec le bénéfice maximal, il faut regarder à quel endroit l’écart entre la droite de la recette et la courbe du coût est le plus grand. D’après le graphique, x₀ = 2.2 centaines d’articles environ.

13) Avec la calculatrice, déterminons l’intervalle (à un article près) pour avoir un bénéfice positif. Pour cela, on a besoin de la formule du bénéfice B(x) qui est égale à
R(x) – C_T(x)
= 7x – (2x² + xe^{-2x + 3})

Je rentre cette formule dans le tableur de la calculatrice.

D’abord de 0 à 1, ensuite de 3 à 4 car nous avions vu dans une question précédente que les bornes étaient environ de 0.6 et de 3.5.

Je commence par mettre le pas (step) à 0.1, la fonction B(x) change de signe entre 0.6 et 0.7, puis entre 3.4 et 3.5.

Puis j’affine le pas au centième pour arriver à l’article près (x étant en centaines d’articles). On a :

B(0.62) = -0.0325 (au dix-millième près)
B(0.63) = 0.0269 (au dix-millième près)

B(3.49) = 0.0046 (au dix-millième près)
B(3.50) = -0.0064 (au dix-millième près)

On conserve les valeurs où les images sont positives.
Donc l’entreprise fait un bénéfice positif
sur l’intervalle [0.63 ; 3.49].

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

f(q) = 0.5q

g(q) = ^{(78 – 6q)}/_{(q + 8)}

1) Pour un prix de 1 euros (en ordonnée), si on trace la droite horizontale de hauteur 1 (d’équation y = 1), la courbe de demande indique une abscisse de 10 millions car le point d’intersection a pour coordonnées (10 ; 1).

Pour un prix de 1 euros (en ordonnée), si on trace la droite horizontale de hauteur 1 (d’équation y = 1), la courbe d’offre indique une abscisse de 2 millions car le point d’intersection a pour coordonnées (2 ; 1).

La demande étant de 10 millions contre une offre de 2 millions, elle est excédentaire.

2) Le prix est de 4.5 euros, donc l’image est de 4.5 euros. Je vais donc déterminer l’antécédent q tel que f(q) = 4.5.
Soit 0.5q = 4.5
⇔ ^0.5q/_0.5 = ^4.5/_0.5
⇔ q = 9

Pour un prix de 4.5, la quantité offerte est de 9 millions.

3) Le prix est de 4.5 euros, donc l’image est de 4.5 euros. Je vais donc déterminer l’antécédent q tel que g(q) = 4.5.
Soit ^{(78 – 6q)}/_{(q + 8)} = 4.5,
⇔ 78 – 6q = 4.5 × (q + 8)
(en multipliant, par (q + 8) positif de chaque côté),
⇔ 78 – 6q – (4.5 × (q + 8)) = 0,
Dans ce cas,
⇔ 78 – 6q – (4.5q + 4,5 × 8) = 0,
⇔ 78 – 6q – 4.5q – 4,5 × 8 = 0,
⇔ 78 – 10.5q – 36 = 0
⇔ 42 – 10.5q = 0
⇔ q = ⁴²/_10.5 = 4.

Si on traces y = 4.5 et on regarde l’intersection avec Cg, on trouve bien un antécédent q qui vaut 4.

Pour un prix de 4.5, la quantité demandée est de 4 millions.

4) Pour un prix de 4.5 euros, comme la quantité demandée est de 4 millions et que la quantité offerte est de 9 millions, il y a trop d’offre par rapport à la demande. Beaucoup de produites seront invendus.

5) Pour avoir le prix d’équilibre, il faut que l’offre soit égale à la demande soit :
f(q) = g(q)
⇔ 0.5q = ^{(78 – 6q)}/_{(q + 8)}
⇔ 0.5q × (q + 8) = 78 – 6q
(en multipliant, par (q + 8) positif de chaque côté),
⇔ 0.5q × q + 0.5q × 8 – 78 + 6q = 0
⇔ 0.5q² + 10q – 78 = 0
⇔ q² + 20q – 156 = 0
(en multipliant, par 2 de chaque côté pour enlever le 0.5)

C’est un polynôme du second degré.
Δ = b² – 4ac
= 20² – 4 × 1 × (-156)
= 400 + 624
= 1024 > 0 soit deux racines :

x₁ = ^{(-b – √Δ)}/_(2a)
= ^{(-20 – √1024)}/_{(2 × 1)}
= ^{(-20 – 32)}/₂
= ^-52/₂
= -26

x₂ = ^{(-b + √Δ)}/_(2a)
= ^{(-20 + √1024)}/_{(2 × 1)}
= ^{(-20 + 32)}/₂
= ¹²/₂
= 6

Comme les quantités vont de 1 à 12, on retient ici q = 6 millions pour quantité d’équilibre.
Le prix d’équilibre est donc g(6) = f(6) = 0.5 × 6 = 3 euros.

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) On a u₀ = 7.

Calcul de u₁ :
u₁
= u₀₊₁ (donc n = 0)
= ^{(2 × u₀ + 6)}/₅ (car n = 0)
= ^{(2 × 7 + 6)}/₅
= 4
Donc u₁ = 4.

Calcul de u₂ :
u₂
= u₁₊₁ (donc n = 1)
= ^{(2 × u₀ + 6)}/₅ (car n = 1)
= ^{(2 × 4 + 6)}/₅
= ¹⁴/₅
Donc u₂ = ¹⁴/₅.

2) Pour savoir si une suite est arithmétique, on calcule déjà les premiers termes, u₀, u₁ et u₂ et on regarde si leur différences sont constantes donc on obtient bien une raison additive r.
On a ici u₁ – u₀ = 4 – 7 = -3
et u₂ – u₁ = ¹⁴/₅ – 4 = ¹⁴/₅ – ²⁰/₅ = ^-6/₅.
u₁ – u₀ est différent de u₂ – u₁, donc la suite (u_n) n’est pas arithmétique car on n’ajoute pas le même nombre pour passer d’un terme au suivant.

Pour savoir si une suite est géométrique, comme les termes sont différents de 0, on calcule ^u₁/_u0 puis ^u₂/_u1.

^u₁/_u0 = ⁴/₇
et
^u₂/_u1 = (¹⁴/₅) / 4
= (¹⁴/₅) / (⁴/₁)
= (¹⁴/₅) × (¹/₄)
= ¹⁴/₂₀
= ⁷/₁₀.

On a ^u₁/_u0 différent de ^u₂/_u1 donc la suite (u_n) n’est pas géométrique car on ne multiplie pas par le même nombre pour passer d’un terme actuel au terme suivant. Il n’y a pas de raison multiplicative constante q pour passer d’un terme actuel au terme suivant.

3) Pour prouver qu’une suite est géométrique, il faut partir de
v_n+1 = …
puis arriver à …
= q × v_n
pour tout entier naturel n.

Comme on sait que u_n+1 = ^{(2u_n + 6)}/₅
et que
v_n = u_n – 2, on peut démarrer par :

v_n+1 = u_n+1 – 2
= ^{(2u_n + 6)}/₅ – 2
= (²/₅) × u_n + ⁶/₅ – ¹⁰/₅
= (²/₅) × u_n – ⁴/₅
= (²/₅) × u_n – ²/₅ × 2
= (²/₅) × (u_n – 2)
= (²/₅) × v_n.

Il existe q réel (q = ²/₅) tel que :
pour tout n, v_n+1 = q × v_n,
donc (v_n) est une suite géométrique de raison ²/₅
et de premier terme v₀ = u₀ – 2 = 7 – 2 = 5.

4) Comme (v_n) est géométrique, pour tout n,
v_n = v₀ × qⁿ
= 5 × (²/₅)ⁿ.

5) Comme v_n = u_n – 2,
alors u_n = v_n + 2,
donc u_n = 5 × (²/₅)ⁿ + 2
et ceci pour tout n entier naturel.

Bonne compréhension,
commenter en cas de point obscur, j’ajouterais une explication,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

Dessinons l’arbre de probabilité avec les données de l’exercice en vert. Comme la probabilité qu’il gagne la première partie est de 0,1, je mets 0,1 vers p(G₁) et
1 – 0,1 = 0,9 vers p(^–G₁).

S’il gagne une partie, la probabilité de gagner la suivante est égale à 0,8. Du coup, c’est un SACHANT et on le mets après la condition du « sachant » (sur une branche de droite). Comme la condition est de gagner la première partie, on met le 0,8 à droite du p(G₁) vers la probabilité de gagner la seconde partie soit p(G₂ ⋂ G₁) (on a gagné à la fois la 1ère et la 2ème partie).
Et du coup, on met le 1 – 0,8 = 0,2 juste en dessous.

On fait de même avec la probabilité de gagner la 2ème partie si on a perdu la première. On est encore dans un SACHANT mais cette fois « sachant » P(^–G₁) car on a perdu la première partie. On place donc le 0,6 après le P(^–G₁) vers la seconde victoire qui est P(G₂ ⋂ ^–G₁) car on a à la fois perdu la 1ère et gagné la seconde. En dessous, on fait 1 – 0,6 = 0,4.

1) On veut maintenant calculer P(G₂). On voit que le G₂ apparaît dans G₂ ⋂ G₁ et G₂⋂^–G₁. Pour arriver à G₂, on doit donc passer par G1 ou ^–G₁.
La rédaction est :
G₁ et ^–G1 forment une partition de l’univers Ω.
D’après la Formule des Probabilités Totales,
P(G₂) = P(G₂ ⋂ G₁) + p(G₂ ⋂ ^–G₁)
= P(G₁) × P(G₂ ⋂ G₁) + p(^–G₁) × P(G₂ ⋂ ^–G₁)
= 0,1 × 0,8 + 0,9 × 0,6 en lisant de gauche à droite (avec les « sachants » à droite).
= 0,08 + 0,54 = 0,62.

2) « Le joueur a gagné la deuxième partie. Calculer la probabilité qu’il ait perdu la première. »
Cela veut dire qu’on SAIT qu’on est en G₂ et on veut ^–G1.
Donc cela revient à calculer P(^–G₁ sachant G₂)
= ^{P(–G₁ ⋂ G₂)}/_P(G2)
= ^{(0,9 × 0,6)}/_0,62 = 0,871.
On a donc P_G2(^–G₁) = 0,871.

3) Pour gagner au moins une partie sur les trois premières, il faut arriver dans l’un de ces trois cas :
– Gagner la 1ère (G₁, peu importe les autres).
– Perdre la 1ère et gagner la 2ème (^–G₁ ⋂ G₂), peu importe la dernière.
– Perdre les deux premières et gagner la 3ème (^–G₁ ⋂ ^–G₂ ⋂ G₃).

Cela revient à faire cet arbre :

On calcule donc :
P(gagner au moins une partie sur les trois)
= 0,1 + 0,9 × 0,6 + 0,9 × 0,4 × 0,6
= 0,64 + 0,216
= 0,856.

4) Pour démontrer cette formule à l’étape n+1 en fonction de l’étape n, il faut dessiner le passage de la partie n à la partie n+1 dans l’arbre de probabilité. Tout d’abord, représente les probabilités de gagner et perdre la partie n à gauche :

Tu peux voir tout à droite que pour avoir P(G_n+1), tu as besoin des ⋂ G_n et ⋂ ^–G_n. Une fois de plus, on utilise la Formule des Probabilités Totales comme ci-dessous :
G_n et ^–G_n forment une partition de l’univers Ω.
D’après la Formule des Probabilités Totales,
p_n+1
= P(G_n+1)
= P(G_n+1 ⋂ G_n) + P(G_n+1 ⋂ ^–G_n)
= p_n × 0,8 + (1 – p_n) × 0,6
= 0,8p_n + 0,6 – 0,6p_n
= 0,2p_n + 0,6
= (¹/₅)p_n + ³/₅.
car 0,2 = ¹/₅ et 0,6 = ³/₅.

5) Pour obtenir un raisonnement par récurrence, il faut utiliser au moins une donnée. Dans le 4) on a démontré que
p_n+1 = (¹/₅)p_n + ³/₅.
Je dois prouver que
p_n = ³/₄ − (¹³/₄) × (¹/₅)ⁿ.

Je commence par l’initialisation avec n = 1 :
D’une part, p₁ = 0,1.
D’autre part,
³/₄ − (¹³/₄) × (¹/₅)¹
= ³/₄ – ¹³/₂₀
= ¹⁵/₂₀ – ¹³/₂₀
= ²/₂₀
= 0,1.

On a bien p = ³/₄ − (¹³/₄) × (¹/₅)¹.
La propriété est vraie au rang 1.

Je dois maintenant faire l’hérédité :
Pour cela, je SUPPOSE que la propriété est vraie au rang n, puis je dois PROUVER qu’elle est vraie au rang n+1.
La supposition devient donc une DONNÉE au sein même de l’hérédité.
On a donc comme données :
p_n+1 = (¹/₅)p_n + ³/₅ (donnée permanente),
p_n = ³/₄ − (¹³/₄) × (¹/₅)ⁿ. (donnée supposée).

On doit donc arriver à la fin à :
p_n+1 = ³/₄ − (¹³/₄) × (¹/₅)ⁿ⁺¹..

Pour cela, on peut partir de p_n+1 = (¹/₅)p_n + ³/₅,
puis remplacer le p_n par la donnée supposée
p_n = ³/₄ − (¹³/₄) × (¹/₅)ⁿ.

On obtient donc
p_n+1 = (¹/₅) × [ ³/₄ − (¹³/₄) × (¹/₅)ⁿ ] + ³/₅
= (¹/₅) × (³/₄) – (¹/₅) × (¹³/₄) × (¹/₅)ⁿ + ³/₅
= ³/₂₀ – (¹³/₅) × (¹/₅)ⁿ × (¹/₅)¹ + ³/₅
= ³/₂₀ + ¹²/₂₀ – (¹³/₄) × (¹/₅)ⁿ⁺¹
= ¹⁵/₂₀ – (¹³/₄) × (¹/₅)ⁿ⁺¹
= ³/₄ – (¹³/₄) × (¹/₅)ⁿ⁺¹

Donc la propriété est vraie au rang (n+1).

6) On a prouvé que p_n = ³/₄ − (¹³/₄) × (¹/₅)ⁿ, calculons la limite.

Quand n tend vers +∞, lim (1/5)ⁿ = 0 car 0 < ¹/₅ < 1.
Par produit, quand n tend vers +∞, lim (¹³/₄) × (¹/₅)ⁿ = 0.
Par différence, quand n tend vers +∞, lim p_n = ³/₄.

7) ³/₄ − p_n < 10^-7
⇔ ³/₄ − (³/₄ – (¹³/₄) × (¹/₅)ⁿ) < 10^-7
⇔ ³/₄ − ³/₄ + (¹³/₄) × (¹/₅)ⁿ < 10^-7
⇔ (¹³/₄) × (³/₅)ⁿ < 10^-7
⇔ (¹/₅)ⁿ < 10^-7 × (⁴/₁₃) en multipliant par ⁴/₁₃ de chaque côté.
Maintenant on peut faire par tâtonnement (ou avec la calculatrice) mais la résolution classique avec le logarithme népérien est :
⇔ ln ((¹/₅)ⁿ) < ln [10^-7 × (⁴/₁₃)] car ln est strictement croissante sur l’intervalle des réels strictement positifs donc on conserve le sens des inégalités.
⇔ n × ln (¹/₅) < ln [10^-7 × (⁴/₁₃)]
car ln(aⁿ) = n × ln(a) d’après le cours.
⇔ n > ln [ 10^-7 × (⁴/₁₃) ] / ln(¹/₅) (on change de sens de l’inégalité car ln(¹/₅) est négatif à la calculette)
⇔ n > 10.7470 environ
⇔ n > 11 car n est entier naturel.

C’est à partir de n = 11 que l’écart entre p_n et ³/₄ devient plus petit que 10^-7.

Bonne compréhension,
Sylvain Jeuland