frenchmaths.com (par Sylvain Jeuland)

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) La dérivée de e^u(x) est u ‘ (x)×e^u(x).
Cela veut dire qu’on dérive ce qu’il y a en haut de l’exponentielle puis on la place devant en coefficient multiplicateur.

La dérivée de x est 1. Donc e^x se dérive en 1×e^x.

La dérivée de 2x est 2. Donc e^2x se dérive en 2×e^2x.

On a f(x) = 2×e^x – e^2x.

Donc f ‘ (x) = 2×1×e^x – 2×e^2x
= 2e^x – 2e^2x

2) On doit partir de notre forme développée (avec un « moins » au milieu) vers une forme factorisée avec un produit de deux facteurs, qui sont 2e^2x et la parenthèse (1 – e^x).

Tout d’abord, e^2x = (e^x)².

Pour prouver une égalité, il est pratique de partir d’un côté du « égal » et arriver à l’autre membre de l’autre côté du « égal ». Développons le membre de droite pour retrouver celui de gauche (sans écrire f ‘ (x)).

2×e^x(1 – e^x)
= 2×e^x×1 – 2×e^x×e^x
= 2×e^x – 2×(e^x)².
= 2×e^x – 2×e^2x
= f ‘ (x)
d’après la dérivée de la question 1).

On a bien f ‘ (x) = 2×e^x(1 – e^x).

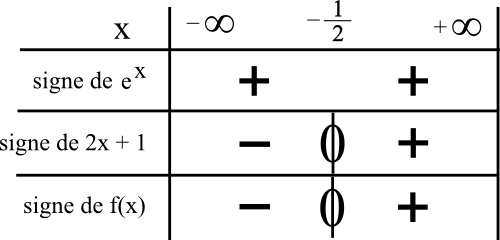
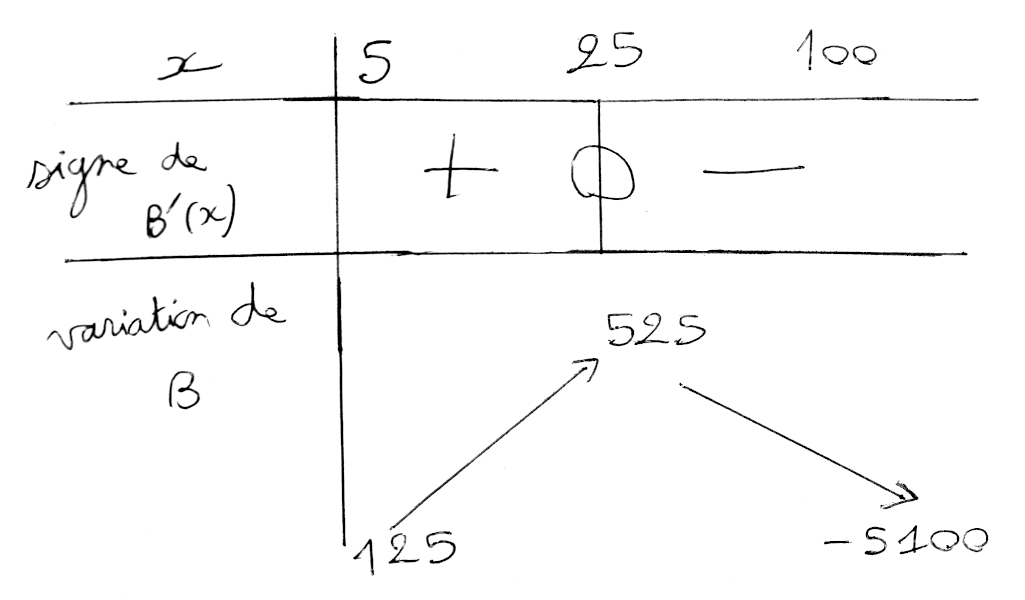
3) Pour obtenir les variations de la fonction f sur R, étudions le signe de f ‘ (x). Pour cela, on utilise la forme factorisée pour faire le tableau de signe suivant.

Nous dévons résoudre l’inéquation 1 – e^x ≥ 0 pour déterminer pour quelles valeurs de x cette expression est positive, on pourra mettre un + pour ces valeurs de x.
1 – e^x ≥ 0
⇔ -e^x ≥ -1
⇔ e^x ≤ 1 (On change le sens de l’inégalité car on divise par le nombre négatif -1 de chaque côté.)
⇔ e^x ≤ e⁰
⇔ x ≤ 0 (car la fonction exponentielle est strictement croissante sur R.)
⇔ x ∈ ]-∞ ; 0]
Soit x à gauche de zéro. On met donc le + à gauche de la valeur x = 0 dans le tableau de signe.

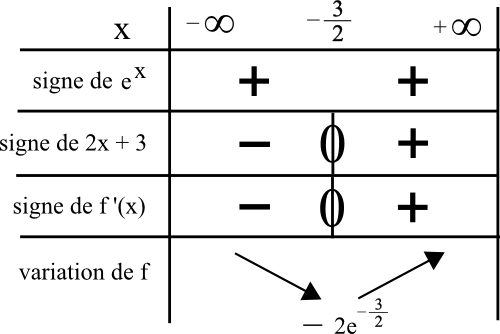
Voici le tableau de signe de f ‘ (x) puis le tableau de variation de f :

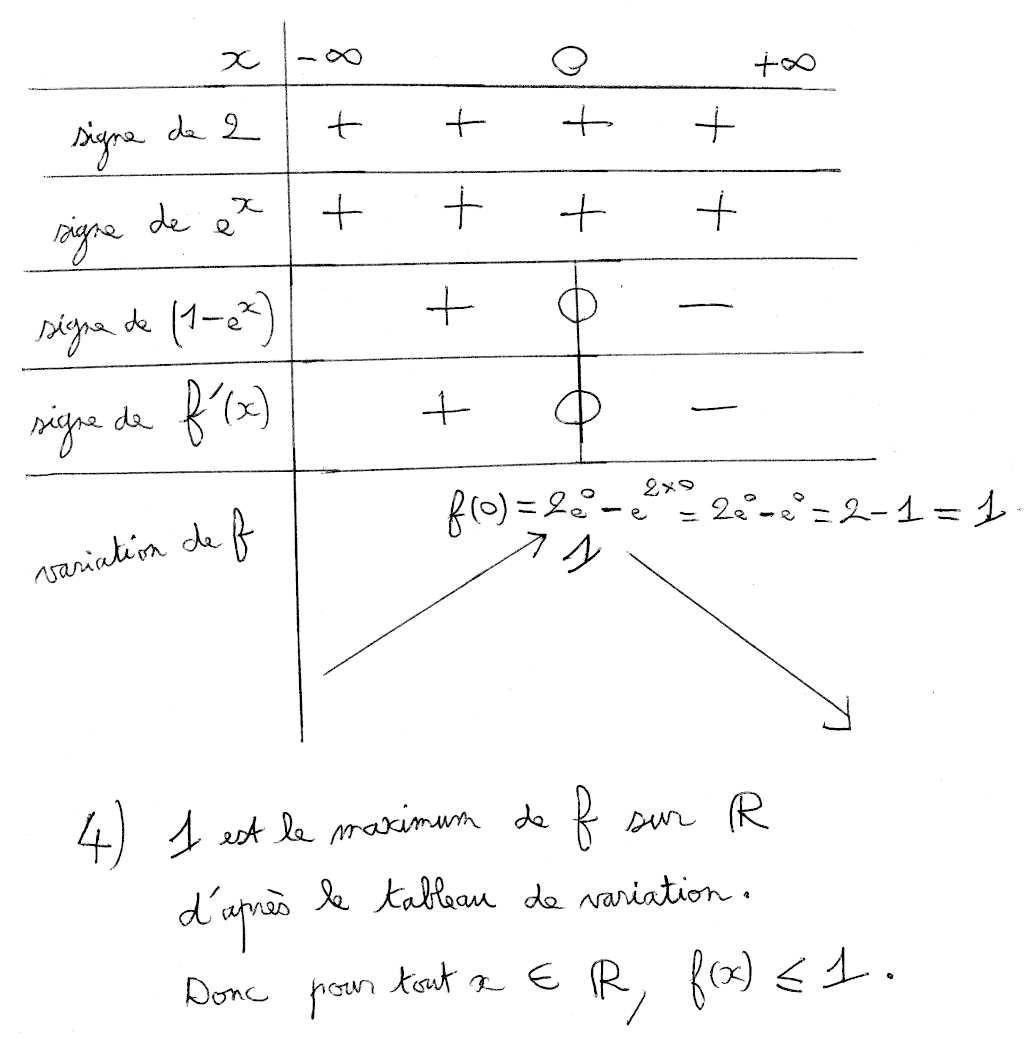
5) La dérivée de e^u(x) est u ‘ (x)×e^u(x).
Cela veut dire qu’on dérive ce qu’il y a en haut de l’exponentielle puis on la place devant en coefficient multiplicateur.

La dérivée de x est 1. Donc e^x se dérive en 1×e^x.

La dérivée de 3x est 3. Donc e^3x se dérive en 3×e^3x.

On a g(x) = 3×e^x – e^3x.

Donc g ‘ (x) = 2-3×1×e^x – 2-3×e^2-3x
= 3e^x – 3e^3x

6) On doit partir de notre forme développée (avec un « moins » au milieu) vers une forme factorisée avec un produit de deux facteurs, qui sont 3e^3x et la parenthèse (1 – e^x).

Tout d’abord, e^3x = (e^x)³.

Pour prouver une égalité, il est pratique de partir d’un côté du « égal » et arriver à l’autre membre de l’autre côté du « égal ». Développons le membre de droite pour retrouver celui de gauche (sans écrire g ‘ (x)).

3×e^x(1 – e^x)
= 3×e^x×1 – 3×e^x×e^x
= 3×e^x – 3×(e^x)³.
= 3×e^x – 3×e^2x
= g ‘ (x)
d’après la dérivée de la question 1).

On a bien g ‘ (x) = 3×e^x(1 – e^x).

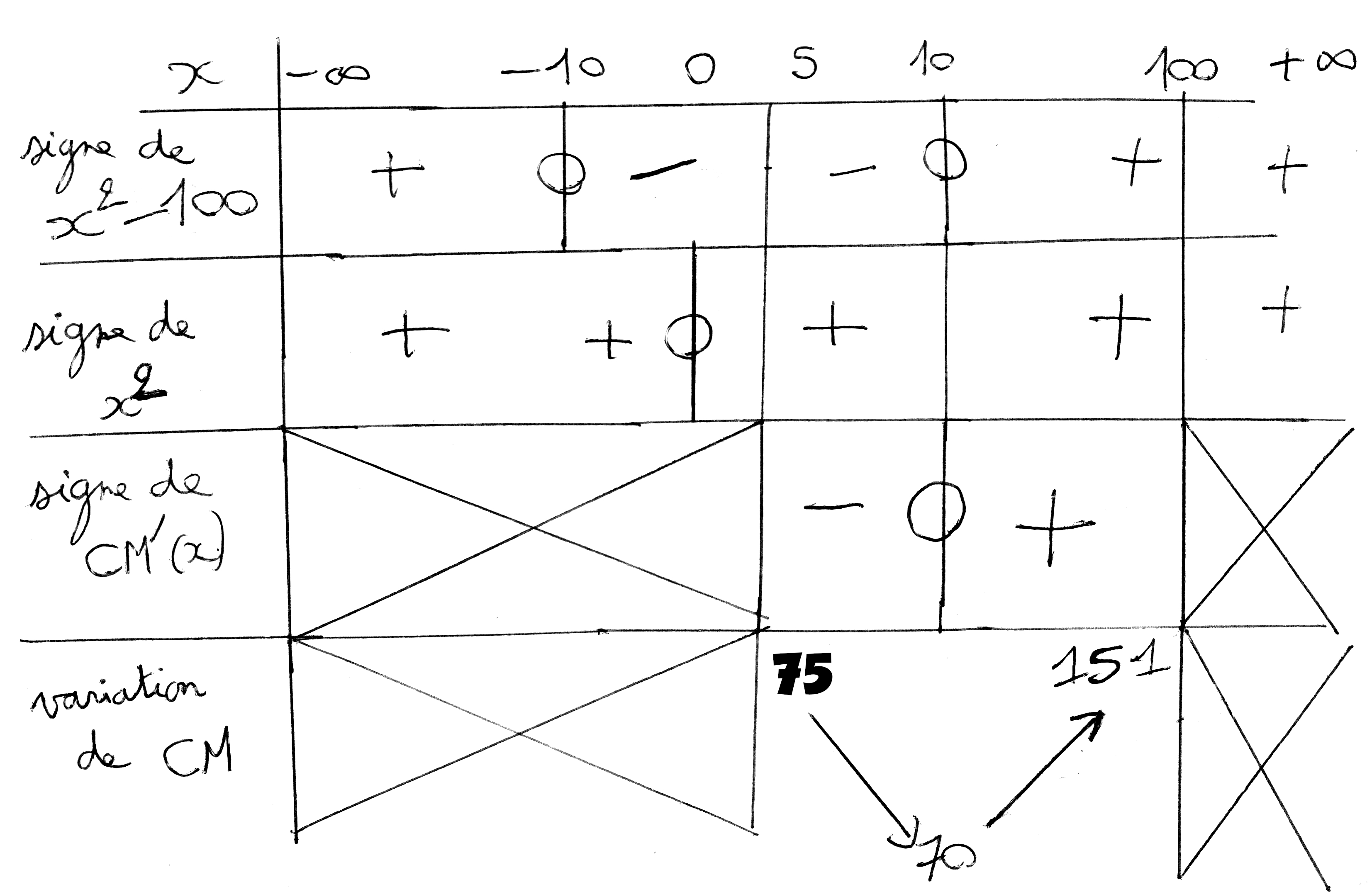
7) Pour obtenir les variations de la fonction g sur R, étudions le signe de g ‘ (x). Pour cela, on utilise la forme factorisée pour faire le tableau de signe suivant.

Nous dévons résoudre l’inéquation 1 – e^2x ≥ 0 pour déterminer pour quelles valeurs de x cette expression est positive, on pourra mettre un + pour ces valeurs de x.
1 – e^2x ≥ 0
⇔ -e^2x ≥ -1
⇔ e^2x ≤ 1 (on change le sens de l’inégalité car on divise par le nombre négatif -1 de chaque côté)
⇔ e^2x ≤ e⁰
⇔ 2x ≤ 0 (car la fonction exponentielle est strictement croissante sur R.)
⇔ x ≤ 0 (On ne change pas le sens de l’inégalité quand on divise par un nombre positif (ici 2) de chaque côté.)
⇔ x ∈ ]-∞ ; 0]
Soit x à gauche de zéro. On met donc le + à gauche de la valeur x = 0 dans le tableau de signe.

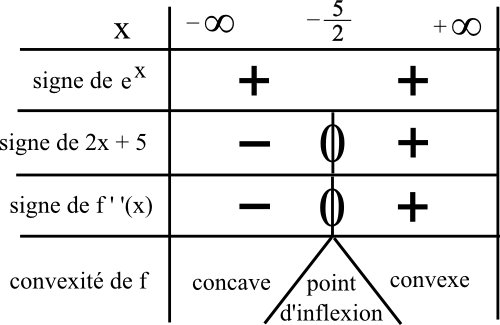
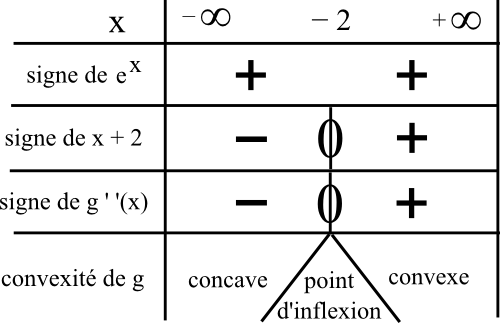
Voici le tableau de signe de g ‘ (x) puis le tableau de variation de g :

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Tout d’abord, pour construire les diagrammes en boîte à moustache, il faut déterminer Q₁, Me et Q₃. Pour ce faire, la première chose à réaliser est le tableau des Effectifs Cumulés Croissants (ECC) en additionnant les effectifs de gauche à droite.

Pierre :
note 1 2 3 4 5
effectif 5 4 2 3 5
ECC 5 9 11 14 19
Le dernier EEC (ici 19) est l’effectif total N de les notes de Pierre.

Wana :
note 1 2 3 4 5
effectif 3 4 6 4 3
ECC 3 7 13 17 20
Le dernier EEC (ici 20) est l’effectif total N de les notes de Wana.

Pour calculer Q₁, on doit trouver la valeur qui se situe à la 0,25×N position. Si cela ne tombe pas sur un nombre entier, on prend juste au dessus. Comme ça, au moins 25% des valeurs sont en dessous de Q₁.

Pierre : 0.25×19 = 4.75, donc on prend la 5ème valeur. D’après le tableau des ECC, elle se situe sous la note 1.
Du coup, Q₁ = 1.

Wana : 0.25×20 = 5, on prend aussi la 5ème valeur. D’après le tableau des ECC, elle se situe sous la note 2 (après la 3ème valeur et avant la 7ème).
Du coup, Q₁ = 2.

Pour calculer Q₃, on doit trouver la valeur qui se situe à la 0,75×N position. Si cela ne tombe pas sur un nombre entier, on prend juste au dessus. Comme ça, au moins 75% des valeurs sont en dessous de Q3.

Pierre : 0.75×19 = 14.25, donc on prend la 15ème valeur. D’après le tableau des ECC, elle se situe sous la note 5 (après la 14ème valeur).
Du coup, Q₃ = 5.

Wana : 0.75×20 = 15, on prend aussi la 15ème valeur. D’après le tableau des ECC, elle se situe sous la note 4 (après la 13ème valeur et avant la 17ème).
Du coup, Q₃ = 4.

Pour la médiane, je vais d’abord considérer le tableau de Pierre.
N = 19, donc la Médiane Me est la valeur centrale.
^N/₂ = 9.5 donc la valeur centrale est la 10ème valeur.

La 10ème valeur se situe en dessous de la note 3 (après la 9ème et avant la 11ème) selon le tableau des ECC de Pierre.
Donc Me = 3.
Cela veut dire qu’au moins 50% des notes de Pierre sont plus petites ou égales à 3 et qu’au moins 50% notes de Pierre sont plus grandes au égales à 3.

Pour la médiane de Wana, l’effectif total N = 20 est pair, il y a donc 2 valeurs centrales.
^N/₂ = 10.
Les deux valeurs centrales sont la 10ème et la 11ème. D’après le tableau des ECC, ces valeurs sont 3 et 3 (après la 7ème valeur et avant la 13ème).
Donc Me = ^{(3 + 3)}/₂ = 3.
Cela veut dire qu’au moins 50% des notes de Wana sont plus petites ou égales à 3 et qu’au moins 50% notes de Wana sont plus grandes au égales à 3.

Pierre : Min = 1, Q₁ = 1, Me = 3, Q₃ = 5, Max = 5.

Wana : Min = 1, Q₁ = 2, Me = 3, Q₃ = 4, Max = 5.

Pour dessiner les diagrammes en boîte, trace d’abord l’axe horizontal en bas avec les valeurs 1, 2, 3, 4 et 5. Puis on fait les boîtes de Q₁ à Q₃, et les lignes qui relient les points Min et Max à la boîte.

2) La moyenne se calcule
x^– = ^{(n₁ × x₁ + n₂ × x₂ + … + n_P × x_P)}/_{(n1 + n2 + … + nP)}.

Pour Pierre :
x^– = ^{(5 × 1 + 4 × 2 + … + 5 × 5)}/_{(5 + 4 + … + 5)}
= ⁵⁶/₁₉
= 2.95

La moyenne de Pierre est de 2.95.

Pour Wana :
x^– = ^{(3 × 1 + 4 × 2 + … + 3 × 5)}/_{(3 + 4 + … + 3)}
= ⁶⁰/₂₀
= 3

La moyenne de Wana est de 3.

Pour calculer l’écart-type, il faut calculer la variance.
Pour ce faire, on calcule les différences des valeurs par rapport à la moyenne :
(x_i – x^–),
– on les met au carré :
(x_i – x^–)²,
et on les multiplie par l’effectif concerné :
n_i×(x_i – x^–)²,
Une fois qu’on a tous ces résultats, on les additionne :
n₁×(x₁ – x^–)²
+ n₂×(x₂ – x^–)²
+ …
+ n_p×(x_p – x^–)²
et on divise le tout par l’effectif total N :

V = ^Somme/_N.

L’écart-type est la racine de la variance : σ = √V.

Comme ici, il n’y a que 5 notes différentes, on n’a pas besoin de passer par la calculatrice, même si c’est bien de vérifier avec l’outil « stastitiques ».

Pour Wana :
3×(1 – 3)²
+ 4×(2 – 3)²
+ 6×(3 – 3)²
+ 4×(4 – 3)²
+ 3×(5 – 3)²
= 3×(-2)² + 4×(-1)² + 6×0² + 4×1² + 3×2²
= 3×4 + 4×1 + 0 + 4×1 + 2×4
= 12 + 4 + 0 + 4 + 8
= 16 + 12 = 28

V_Wana = ²⁸/₂₀ = 1,4.

σ_Wana = √1,4 = 1,18.

Pour Pierre :
5×(1 – 2.95)²
+ 4×(2 – 2.95)²
+ 2×(3 – 2.95)²
+ 3×(4 – 2.95)²
+ 5×(5 – 2.95)²
= 5×(-1.95)² + 4×(-0.95)² + 2×0.05² + 3×1.05² + 5×2.05²
= 5×3.8025 + 4×0.9025+ 2×0.0025 + 3×1.1025 + 5×4.2025
= 19.0125 + 3.61 + 0.005 + 3.3075 + 21.0125
= 46,9475

V_Pierre = ^46,9475/₁₉ = 2,471.

σ_Pierre = √2,471 = 1,572.

3) Les résultats de Pierre sont plus dispersés que ceux de Wana car son écart interquartile et son écart-type sont plus grands que ceux de Wana. Bien que les médianes sont les mêmes la moyenne de Pierre est un peu en dessous de celle de Wana.

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

f(x) = (2x + 1)e^x

1) Pour déterminer le signe du produit f(x), qui a deux facteurs, on construit un tableau de signe avec chacun des facteurs.

Un exponentiel est toujours strictement positif quelque soit son contenu donc on met un unique + dans la ligne de l’exponentielle.

On met un « + » pour 2x + 1
⇔ 2x + 1 ≥ 0
⇔ 2x ≥ -1
⇔ x ≥ –¹/₂
⇔ on est à droite de –¹/₂ dans la première ligne du tableau de signe.
Donc on met le « + » à droite du « 0 » en dessous de –¹/₂.

On obtient donc le tableau suivant :

2) Pour déterminer les variations d’une fonction, on détermine d’abord le signe de la fonction dérivée.

f(x) = (2x + 1)e^x
= u(x) × v(x)

avec
u(x) = 2x + 1,
u ‘ (x) = 2,
v(x) = e^x,
v ‘ (x) = e^x.

La dérivée du produit f(x) est donc la formule :
f ‘ (x) = u ‘ (x) × v(x) + u(x) × v ‘ (x)

Du coup, f ‘ (x) = 2×e^x + (2x + 1)×e^x
= e^x × (2 + (2x + 1)) (en factorisant par l’exponentiel)
= e^x × (2x + 3)

Pour déterminer le signe du produit f ‘ (x), qui a deux facteurs, on construit un tableau de signe avec chacun des facteurs.

Un exponentiel est toujours strictement positif quelque soit son contenu donc on met un unique + dans la ligne de l’exponentielle.

On met un « + » pour 2x + 3
⇔ 2x + 3 ≥ 0
⇔ 2x ≥ -3
⇔ x ≥ –³/₂
⇔ on est à droite de –³/₂ dans la première ligne du tableau de signe.
Donc on met le « + » à droite du « 0 » en dessous de –³/₂.

On obtient donc le tableau suivant :

Le minimum est atteint en –³/₂.
On calcule f(-³/₂) en remplaçant x par –³/₂dans l’expression de f(x).

3) Déterminons notre dérivée seconde f ‘ ‘ (x) :

f ‘ (x) = (2x + 3) × e^x
= u(x) × v(x)

avec
u(x) = 2x + 3,
u ‘ (x) = 2,
v(x) = e^x,
v ‘ (x) = e^x.

La dérivée du produit f ‘ (x) est donc la formule :
f ‘ ‘ (x) = u ‘ (x) × v(x) + u(x) × v ‘ (x)

Du coup, f ‘ ‘ (x) = 2×e^x + (2x + 3)×e^x
= e^x × (2 + (2x + 3)) (en factorisant par l’exponentiel)
= e^x × (2x + 5)

Pour déterminer le signe du produit f ‘ ‘ (x), qui a deux facteurs, on construit un tableau de signe avec chacun des facteurs.

Un exponentiel est toujours strictement positif quelque soit son contenu donc on met un unique + dans la ligne de l’exponentielle.

On met un « + » pour 2x + 5
⇔ 2x + 3 ≥ 0
⇔ 2x ≥ -5
⇔ x ≥ –⁵/₂
⇔ on est à droite de –⁵/₂ dans la première ligne du tableau de signe.
Donc on met le « + » à droite du « 0 » en dessous de –⁵/₂.

On obtient donc le tableau suivant :

(On ne tiendra pas compte de la dernière ligne du tableau concave / point d’inflexion / convexe.)

4) L’équation d’une tangente à une courbe Cf au point d’abscisse a est :

Ici, a = –⁵/₂.

L’ordonnée f(a) est égale à f(-⁵/₂) =
= (2 × –⁵/₂ + 1)e^–5/₂
= (-5 + 1)e^–5/₂
= -4e^–5/₂.

Donc f(a) = -4e^–5/₂

De plus,
f ‘ (a) = (2 × –⁵/₂ + 3)e^–5/₂
= (-5 + 3)e^–5/₂
= -2e^–5/₂.

Du coup, l’équation de la tangente au point d’inflexion est :

y = -2e^–5/₂(x – (-⁵/₂)) + (-4e^–5/₂)
= -2e^–5/₂ × x + (-2) × e^–5/₂ × ⁵/₂ – 4e^–5/₂
= -2e^–5/₂ × x – 5e^–5/₂ – 4e^–5/₂
= -2e^–5/₂ × x – 9e^–5/₂

5) Calculons g ‘ (x) :

g(x) = x × e^x
= u(x) × v(x)

avec
u(x) = x,
u ‘ (x) = 1,
v(x) = e^x,
v ‘ (x) = e^x.

La dérivée du produit g ‘ (x) est donc la formule :
g ‘ (x) = u ‘ (x) × v(x) + u(x) × v ‘ (x)
= 1 × e^x + x × e^x
= e^x × (1 + x).

6) Calculons g ‘ ‘ (x) :

g ‘ (x)
= a(x) × b(x)

avec a(x) = e^x
a ‘ (x) = e^x
b(x) = 1 + x
b ‘ (x) = 1

g ‘ ‘ (x) = a ‘ (x) × b(x) + a(x) × b ‘ (x)
= e^x × (1 + x) + e^x × 1
= e^x × (1 + x + 1)
= e^x × (x + 2)

Pour déterminer le signe du produit g ‘ ‘ (x), qui a deux facteurs, on construit un tableau de signe avec chacun des facteurs.

Un exponentiel est toujours strictement positif quelque soit son contenu donc on met un unique + dans la ligne de l’exponentielle.

On met un « + » pour x + 2
⇔ x + 2 ≥ 0
⇔ x ≥ -2
⇔ x ≥ -2
⇔ on est à droite de -2 dans la première ligne du tableau de signe.
Donc on met le « + » à droite du « 0 » en dessous de -2.

On obtient donc le tableau suivant :

(On ne tiendra pas compte de la dernière ligne du tableau concave / point d’inflexion / convexe.)

7) Calculons h ‘ (x) :

h(x) = ^ex/_{(x – 1)}
= ^u(x)/_v(x)

avec u(x) = e^x,
u ‘ (x) = e^x,
v(x) = x – 1,
v ‘ (x) = 1.

h ‘ (x)
= ^{(ex× (x – 1) – ex × 1)}/_{(x – 1)²}
= ^{(ex(x – 2))}/_{(x – 1)²}

8) É tudions k(x) = 0,9^x :

0,9 est positif, donc n’importe quelle puissance de 0,9 est positive, donc k positive sur R.
0,9 < 1 donc (0,9^x) est strictement décroissante sur R.

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Pour donner l’expression du bénéfice, il faut écrire
B(x)= R(x) – C(x)
avec R(x) = prix_unitaire×quantité = 100 × x = 100x.

Donc B(x) = 100x – (x² + 50x + 100)
= 100x – (x² + 50x + 100)
= -x² + 50x – 100.

Donc le bénéfice horaire réalisé par la fabrication et la vente de x appareils est B(x) = -x² + 50x – 100 pour x appartenant à [5 ; 100].

2) Calcul de la dérivée :

On a B(x) = -x² + 50x – 100.

La dérivée de -x² est -2x.
La dérivée de 50x est le coefficient devant le x soit 50.
Le coefficient d’une constante (ici -100) est 0.

Donc B ‘ (x) = -2x + 50.

Étudions le signe B ‘ (x) pour obtenir les variations de B :

Pour déterminer le signe de B ‘ (x), ma méthode est de résoudre une inéquation avec ≥ 0 car nous sommes dans le cas d’une fonction affine (cela fonctionne aussi avec les fonctions exponentielles et logarithmes népérériens). Cela permet de déterminer si on met le + à gauche ou à droite de la valeur annulante.

B ‘ (x) ≥ 0 (on cherche donc où mettre le + dans le tableau de signes)
⇔ -2x + 50 ≥ 0
⇔ -2x ≥ -50
⇔ x ≤ 25 (comme on divise par un négatif, on change le sens de l’inégalité)

Les x ≤ 25, cela correspond aux « x » sont à gauche de 25.
Donc, on mettra le + quand « x » sera à gauche de 25.

B(5) = -5² + 50×5 – 100
= -25 + 250 – 100
= 225 – 100
= 125.

B(25) = -25² + 50×25 – 100
= -625 + 1250 – 100
= 625 – 100
= 525.

B(100) = -100² + 50×100 – 100
= -10000 + 5000 – 100
= -5000 – 100
= -5100.

3) Le nombre d’appareils à produire pour obtenir un bénéfice maximal est donc 25 et ce bénéfice est 525 car c’est le maximum atteint par la fonction B dans le tableau de variation. Il est atteint en x = 25.

4) C(x) = x² + 50x + 100
et CM(x) = ^C(x)/_x
Donc CM(x) = ^{(x² + 50x + 100)}/_x
= ^x²/_x + ^50x/_x + ¹⁰⁰/_x
= x + 50 + ¹⁰⁰/_x.

5) CM(x)
= x + 50 + ¹⁰⁰/_x
= x + 50 + ^u(x)/_v(x)
avec
u(x) = 100,
u ‘ (x) = 0,
v(x) = x,
v ‘ (x) = 1.

Donc CM ‘ (x)
= 1 + 0 + ^{[ u ‘ (x)×v(x) – u(x)×v ‘ (x) ]}/_(v(x))²
= 1 + ^{[ 0×x – 100×1 ]}/_(x²)
= 1 – ¹⁰⁰/_(x²)
= ^x²/_x² – ¹⁰⁰/_x²
= ^{(x² − 100)}/_x².

6) CM ‘ (x) est un quotient composé d’un polynôme du second degré au numérateur, et d’un carré au dénominateur.

Etudions le signe du polynôme au numérateur :

Pour étudier le signe de ce polynôme du second degré, on calcule le discriminant.

Δ = b² – 4×a×c
= 0² – 4×1×(-100)
= 400 > 0 donc deux racines.

x₁ = ^{(-b – √Δ})/_(2a)
= ^{(-0 – √400)}/_(2×1)
= ^{(-0 – 20})/₂
= ^-20/₂
= -10.

x₂ = ^{(-b + √Δ})/_(2a)
= ^{(-0 + √400)}/_(2×1)
= ^{(-0 + 20})/₂
= ²⁰/₂
= 10.

Comme a = 1 > 0, la parabole est ouverte vers le haut (souriante car atmosphère et ambiance positives).
De plus, comme Δ > 0, elle coupe deux fois l’axe des abscisses.
Donc ce polynôme du second degré est donc positif, puis négatif, puis positif.

Voici donc le tableau de signe de CM ‘ (x) et de variation de CM :

CM(5) = 5 + 50 + ¹⁰⁰/₅
= 55 + 20
= 75.

CM(10) = 10 + 50 + ¹⁰⁰/₁₀
= 60 + 10
= 70.

CM(100) = 100 + 50 + ¹⁰⁰/₁₀₀
= 150 + 1
= 151.

7) D’après le tableau de variation précédent, CM est minimal pour x = 10 et son minimum est 70.

8) B est maximal pour x = 25 et CM est minimal pour x = 10. Donc le bénéfice n’est pas maximal quand le coût moyen est minimal.

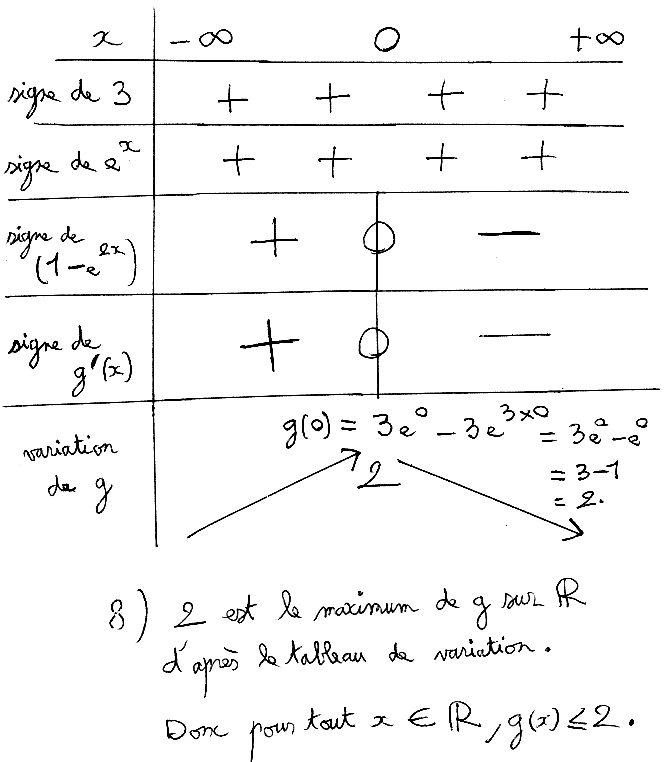
Bonne compréhension,
Sylvain Jeuland