Maths de terminale : exercice de complexes avec suite géométrique, angles, points, somme de termes, forme trigonométrique, distances, limite.
Exercice N°502 :
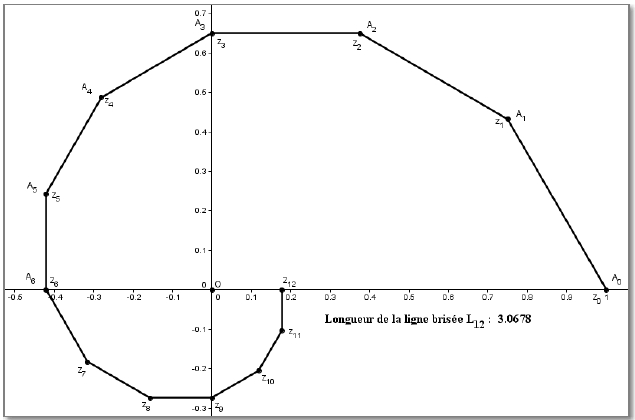
Le plan complexe est muni d’un repère orthonormé (O ; →u ; →v).
On considère les nombres complexes zn définis, pour tout entier naturel n,
par z0 = 1
et
zn+1 = ( 3/4 + i√3/4 )×zn.
On note An le point d’affixe zn.
1) Donner la forme trigonométrique et la forme exponentielle du nombre complexe a = 3/4 + i√3/4.
2) Montrer que, pour tout entier naturel n ∈ N,
OAn+1 = (√3/2)×OAn.
En déduire la longueur OAn en fonction de n.
3) Montrer que, pour pour tout n ∈ N,
(→OAn ; →OAn+1) = π/6 ( modulo 2π )
et
(→An+1O ; →An+1An) = π/2 ( modulo 2π ).
4) En déduire une construction rapide, sur la figure ci-dessus, des 12 points suivants A13 jusqu’à A24. (Expliquez votre méthode).
5) Exprimer l’angle (→OA0 ; →OAn) en fonction de n et en déduire pour quelles valeurs de n, les points O, A0 et An sont alignés.
On désire calculer la longueur de la ligne polygonale de sommets successifs A0, A1, …, An.
On note cette longueur Ln = Σ[k de 0 à n−1]AkAk+1.
5) Montrer que AkAk+1 = ∣a − 1∣×OAk.
6) En déduire Ln en fonction de n. (On utilisera la formule de la somme géométrique).
7) Déterminer la limite de Ln quand n tend vers +∞.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, complexes, suite géométrique.
Exercice précédent : Complexes – Degré 3, triangle, vecteurs, droite, cercle – Terminale


L’exercice N°502, c’est vraiment fantastique car c’est ma culture, merci
Votre culture ? Laquelle ?