frenchmaths.com (par Sylvain Jeuland)

Exercice : Clic droit vers l’exercice

Tout le corrigé :

f(x) = ^{(2x – 4)}/_{(x + 2)}

1) Déterminer le domaine de définition Df de f :

f(x) est un quotient.
Un quotient est défini quand son dénominateur est différent de 0.
Pour déterminer les valeurs exclues (s’il y en a),
résous l’équation dénominateur = 0.
x + 2 = 0
⇔ x = -2.
Donc -2 est une valeur exclue (ou interdite).
Du coup, on ne peut pas choisir -2 pour x, car cela reviendrait à diviser par 0.
Donc Df = ]-∞ ; -2[ ⋃ ]-2 ; +∞[.
Df = R privé de {-2}.

2) Montrer que pour tout réel x de Df,
f(x) = 2 – ⁸/_{(x + 2)} :

Pour démontrer une telle égalité, on part de la forme développée (celle avec le « moins ») puis on tente d’arriver à la forme « quotient » (celle de l’énoncé). Donc :

2 – ⁸/_{(x + 2)}
= 2×^{(x + 2)}/_{(x + 2)} – ⁸/_{(x + 2)} (en mettant au même dénominateur).
= ^{(2x + 4)}/_{(x + 2)} – ⁸/_{(x + 2)} (en distribuant le 2 au 1er numérateur).
= ^{(2x + 4 – (8))}/_{(x + 2)} (en rassemblant les numérateurs)
= ^{(2x – 4)}/_{(x + 2)}
= f(x) (qu’on met seulement à la fin).

On a donc bien démontré que f(x) = 2 – ⁸/_{(x + 2)}.

A la main, cela donne :

3) Étudier les variations de f sur ]-2 ; +∞[ :

Méthode 1 :

Pour démontrer qu’une fonction est croissante en seconde, la propriété du cours dit qu’il faut :

– Partir de a < b. C’est à dire écrire « a < b » sur la feuille.
– Puis arriver à f(a) ≤ f(b).

En effet, si « a < b donne f(a) ≤ f(b)« , cela veut dire que la fonction f est croissante comme c’est illustré sur l’image ci-dessous.

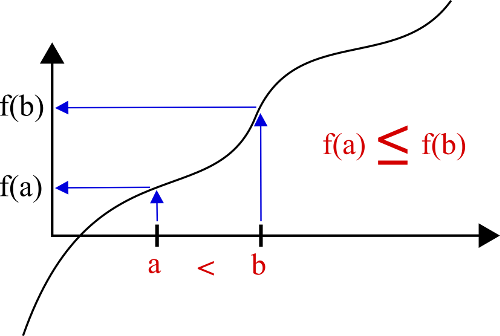
On voit bien que si on prend a < b et qu’on arrive à f(a) ≤ f(b), alors la courbe monte entre les deux points.
Attention, il faut dire « pour tout a et b tels que a < b« .

Reprenons la formule f(x) = 2 – ⁸/_{(x + 2)}.

Rédaction de la méthode 1 :

Sur ]-2 ; +∞[ :
Pour tout a et b tels que : -2 < a < b (-2 est exclu donc a > -2), on a :

-2 < a < b

⇔ -2+2 < a+2 < b+2 (on ajoute déjà le +2 à côté du « x » au dénominateur de f(x))

⇔ 0 < a+2 < b+2
⇔ ¹/_{(a + 2)} > ¹/_{(b + 2)} (on passe à l’inverse, et comme la fonction « inverse » est strictement décroissante sur ]0 ; +∞[, on change le sens de l’inégalité « < » en « > »).
On ne s’occupe plus du 0 car on ne peut pas inverser 0.

⇔ ⁸/_{(a + 2)} > ⁸/_{(b + 2)} (en multipliant par 8 positif, on garde le sens de l’inégalité).

⇔ –⁸/_{(a + 2)} < –⁸/_{(b + 2)} (en multipliant par « -« , on change le sens de l’inégalité).

⇔ 2 – ⁸/_{(a + 2)} < 2 – ⁸/_{(b + 2)} (l’ajout ou la soustraction ne change pas le sens)

⇔ f(a) < f(b)

On a donc « a < b donne f(a) < f(b) » ou même « a < b donne f(a) ≤ f(b) » avec une inégalité large. Donc la fonction f est croissante sur ]-2 ; +∞[.

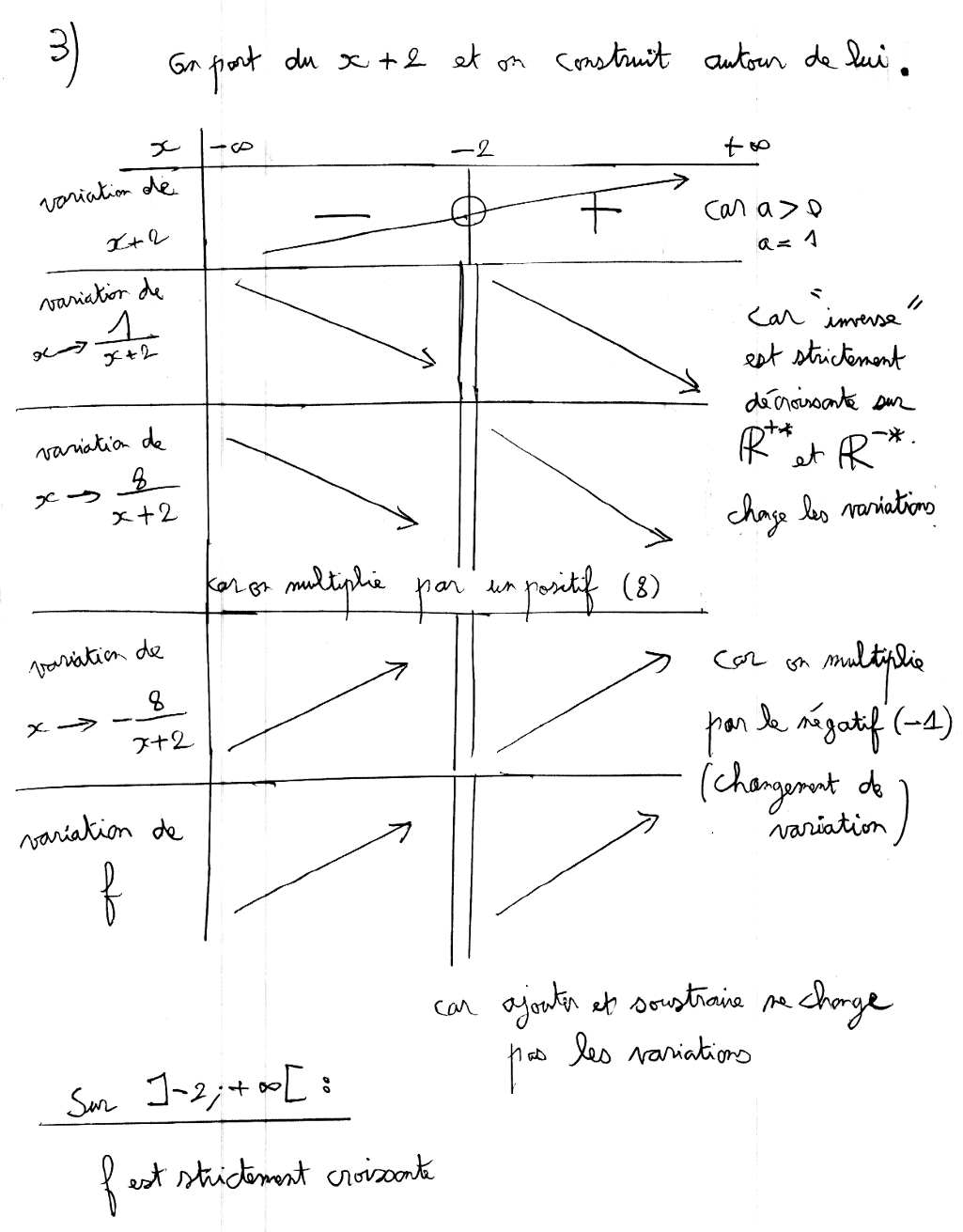
Rédaction de la méthode 2 :

Bonne compréhension,
Sylvain Jeuland