Exercice : Clic droit vers l’exercice
Tout le corrigé :
1) Rédaction :
Pour avoir les variations de f, faisons la dérivée f'(x).
f(x) = (u(x))/(v(x))
avec u(x) = x2 + 2,
donc u'(x) = 2x + 0 = 2x,
v(x) = 1 − 2x,
donc v'(x) = 0 – 2 = -2.
Du coup, f'(x) = (u'(x)×v(x) – u(x)×v'(x))/(v(x))2
= (2x×(1 − 2x) – (x2 + 2)×(-2))/(1 − 2x)2
= (2x − 4x2 – [-2x2 – 4])/(1 − 2x)2
= (2x − 4x2 + 2x2 + 4)/(1 − 2x)2
= (−2x2 + 2x + 4)/(1 − 2x)2.
Pour étudier le signe de f'(x), on fait un tableau de signe avec chaque facteur et diviseur. L’un est −2x2 + 2x + 4 et le diviseur est (1 − 2x)2
Un carré est toujours positif ou nul. Donc (1 − 2x)2 est toujours strictement positif ou nul quand 1-2x vaut 0. Cela arrive quand x=1/2. En cette valeur, le carré est nul, mais comme il est au dénominateur, cela fera une double-barre dans le tableau de f'(x) car la fraction n’est pas définie pour x=1/2.
Pour le signe de −2x2 + 2x + 4, qui est du second degré, on fait :
Δ = b2 – 4ac
= 22 – 4 × (-2) × 4
= 4 + 32 = 36 > 0.
Donc deux racines :
x1 = (-b – √Δ)/(2a)
= (-2 – √36)/(2 × (-2))
= (-2 – 6)/(-4)
= -8/-4
= 2
x2 = (-b + √Δ)/(2a)
= (-2 + √36)/(2 × (-2))
= (-2 + 6)/(-4)
= 4/12-4
= -1
a = -2 donc le trinôme est négatif à l’extérieur des racines -1 et 2. Du coup, on obtient le tableau suivant :
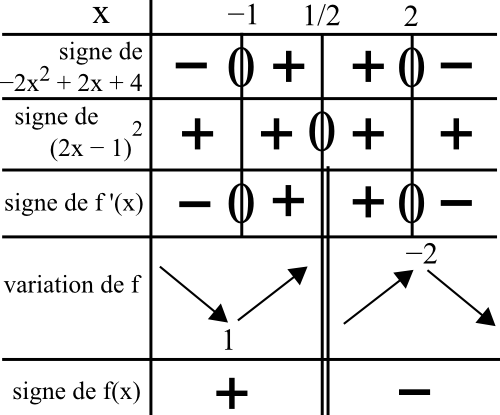
J’ai aussi déterminé le signe de f(x) à l’aide des variations et des valeurs.
2) Rédaction :
L’équation d’une tangente est :

Donc en a = 0,
y = f'(0) (x – 0) + f(0).
f'(0) = (−2×02 + 2×0 + 4)/(1 − 2×0)2
= 4/12
= 4
f(0) = (02 + 2)/(1 – 2×0)
= 2/1
= 2
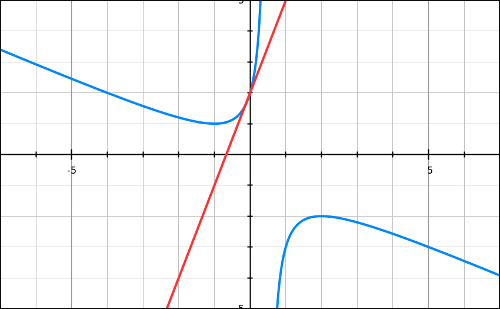
Donc l’équation de la tangente à Cf au point d’abscisse 0 est
y = 4(x – 0) + 2 = 4x + 2.
3) Rédaction :
g est déjà continue sur chacun des intervalles séparément (f est rationnelle définie avant 0 et 3x + m est affine). Il faut donc juste faire en sorte que g soit continue en 0.
Pour que g soit continue en 0, il faut que la limite de g(x) en 0 « -moins » et 0 « +plus » soit la même, et qu’elles soient égales à g(0).
Quand l’un des deux côtés est défini, ici c’est le cas pour 0 à gauche car la borne 0 de l’intervalle ]-∞ ; 0] est fermée, la limite est juste l’image.
Donc limite de g(x) quand x tend vers 0 « -moins » = g(0) = f(0) = 2 (expression de la première ligne).
Pour la limite à droite en 0 « +plus », il faut donc trouver m tel qu’elle soit égale à 2 (qui est l’image g(0)) pour que la fonction g soit continue en 0.
lim [x → 0+] 3x = 0
lim [x → 0+] m = m
Par somme, lim [x → 0+] (3x + m) = m
Donc lim [x → 0+] g(x) = m
Pour que c’est limite à droite soit égale 2, m doit être égal à 2.
Donc m = 2.
4) Rédaction :
Déjà g est dérivable sur ]-∞ ; 0] car elle vaut f qui est dérivable avec comme dérivée en 0, f'(0) = 2.
Sur ] 0 ; +∞ [, g est affine donc la dérivée est le coefficient directeur 3.
La limite en zéro à droite de la dérivée est donc 3.
Or à gauche g'(0) = 2, à droite la limite de g’ en 0+ est 3. Les valeurs sont différentes donc g n’est pas dérivable en 0.
Bonne compréhension,
Sylvain Jeuland