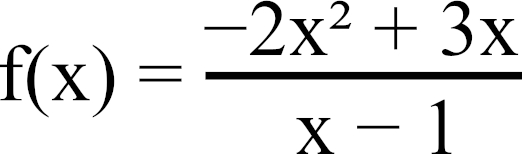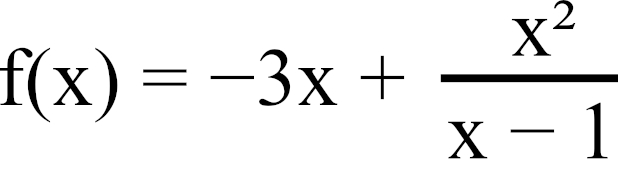Des centaines d'exercices de DS

Fonctions Suites Géométrie Vecteurs Pourcentages Dérivées Expo LN Intégrales Complexes

Essaie les exercices de DS, clique ci-dessous

Choisis ton exercice de DS !

Exercice, arbre, suite géométrique. Maths de terminale avec les probabilités conditionnelles. Raison, premier terme, limite, algorithme.

Exercice N°321 :

Probas, suites, conditionnelle, arbre, géométrique, terminale

Exercice N°321 :

Dans un stand de tir, un tireur effectue des tirs successifs pour atteindre plusieurs cibles.
La probabilité que la première cible soit atteinte est 1/2.
Lorsqu’une cible est atteinte, la probabilité que la suivante le soit est 3/4.
Lorsqu’une cible n’est pas atteinte, la probabilité que la suivante soit atteinte est 1/2.

On note, pour tout entier naturel non nul n,
An l’événement « la n-ième cible est atteinte ».
–An l’événement « la n-ième cible n’est pas atteinte ». – est « barre ».
an la probabilité de l’événement An.
bn la probabilité de l’événement –An.

1) Calculer a1 et b1, puis calculer a2 et b2 (on pourra utiliser un arbre pondéré). Lis la suite »

Ecris le premier commentaire

Maths de première : exercice sur les fonction, variation, signe. Ensemble de définition, images, antécédents, tableaux, équations, courbe.

Exercice N°319 :

Cf et Cg représentent deux fonctions.

Exercice, fonction, variation, signe images, antécédents, première

1) Sur quel ensemble D ces fonctions sont-elles définies ?

2) Quelle est l’image de -4 par f ? par g ? Lis la suite »

Ecris le premier commentaire

Exercice de maths de première sur une fonction rationnelle, graphique, antécédent, image, affine, courbes représentatives, intersection.

Exercice N°316 :

Fonctions, rationnelle, affine, graphique, antécédent, première

L’offre et la demande désignent respectivement la quantité d’un bien ou d’un service que les acteurs du marché sont prêts à vendre ou à acheter à un prix donné.
Une étude concernant un article A a permis d’établir que :
– la fonction d’offre f est donnée par :
f(q) = 0.5q,
– la fonction demande g est donnée par
g(q) = (78 – 6q)/(q + 8),
où f(q) et g(q) sont les prix d’un article en euros, pour une quantité q comprise entre 1 et 12 millions d’unités.

1) À l’aide du graphique précédent et en argumentant la réponse, déterminer si la demande est excédentaire quand le prix de vente d’un article est de 1 euro. Lis la suite »

Ecris le premier commentaire

Maths de première : inéquations sur quotients avec second degré. Expressions rationnelles, tableaux de signe, inégalité, fractions.

Exercice N°315 :

Inéquations, quotients, second degré, signe, intervalle, inverse, première

Exercice N°315 :

1) La somme d’un nombre et de son inverse est 5,2. Quel est ce nombre ? Lis la suite »

Ecris le premier commentaire

Maths de terminale : exercice d’exponentielle avec suite de fonctions. Limite, courbe, tangente, équation, dérivée, point, coordonnées.

Exercice N°285 :

Exponentielle, famille, fonctions, tangente, terminale

Exercice N°285 :

On considère, pour tout n ∈ N, la famille de fonctions fn définie sur R par :
fn(x) = e-nx/(ex + 1).

On note Cn sa courbe représentative dans un repère orthonormal avec comme unité graphique 10 cm. On note I le point de coordonnées (0 ; 1/2).

Étude du cas où n = 0 :

1) Étudier les limites de f0 en +∞ et en −∞. Lis la suite »

Ecris le premier commentaire

Maths de première sur les fonctions ; exercice de coût, recette, bénéfice. Calcul de quantité. Résolution graphique et par le calcul.

Exercice N°313 :

Exercice, coût, recette, bénéfice, fonction, polynôme, droite, première

Une entreprise fabrique x quintaux d’un certain produit, x étant compris entre 0 et 8. On suppose que toute la production est vendue.
Le coût total de fabrication, exprimé en milliers d’euros, est fonction de la quantité produite. On le note C(x), C étant la fonction coût total dont la représentation graphique Cf dans un repère orthogonal est donnée ci-dessus. C est définie par
C(x) = -x3 + 11x2 + 16x + 20.

1-2) Déterminer par lecture graphique :

1) Le coût de fabrication, en euros, de 8 quintaux de ce produit. Lis la suite »

Ecris le premier commentaire

Maths de première : exercice de variation avec composée de fonctions. Domaine de définition, racine carrée, polynôme, second degré, inverse.

Exercice N°312 :

Exercice, variation, composée de fonctions, racine, trinôme, première

Exercice N°312 :

Soient u et v définies par
u(x) = -x2 + 2x + 3
pour x ∈ R
et
v(x) = -3√x + 1
pour x ∈ [0 ; +∞[.

1) Pour quelles valeurs de x peut-on définir la composée u suivie de v ? Détailler précisément la démarche et les calculs. On notera D cet ensemble de définition. Lis la suite »

Ecris le premier commentaire

Maths de première : exercice de fonction. variation, courbe. Intervalle, tableau de variation, signe, image, carré, racine, maximum.

Exercice N°311 :

Exercice, fonction, variation, courbe

1) La fonction f est croissante sur quel intervalle :
a) [-3 ; -1] ?
b) [-1 ; 1] ?
c) [-3 ; -2] ?
d) Ou [-2 ; 1] ? Lis la suite »

Ecris le premier commentaire

Maths de terminale : exercice de limite avec fonction rationnelle, asymptote, variation, domaine de définition, courbe représentative.

Exercice N°706 :

Exercice, limite, fonction rationnelle, asymptote, variation, terminale

Exercice N°706 :

On considère la fonction f par
f(x) = (x3 + 1)/(x − 1).

1) Déterminer son domaine de définition le plus étendu appelé Df. Lis la suite »

2 commentaires

Exercice de maths de première sur une fonction rationnelle (exercice corrigé). Coefficients, position, dérivées, tableau, variations.

Exercice N°057 :

Fonction rationnelle, variation, tangente, équation, première, exercice corrigé

Exercice N°057 :

Soit f la fonction définie sur R privé de { 1 } par

Fonction rationnelle, variation, tangente, équation, première, exercice corrigé
.
C est sa courbe représentative.

1) Vérifier que, pour x différent de 1,

Fonction rationnelle, variation, tangente, équation, première, exercice corrigé
. Lis la suite »

Ecris le premier commentaire

« Articles précédents     Articles suivants »
✕
FrenchMaths.com

GRATUIT
VOIR