Maths : exercice sur le Nombre d’Or de première. Second degré, parabole, trajectoire, sommet, tableau de variation, forme canonique.
Exercice N°799 :

Exercice N°799 :
On considère les deux réels Φ = (1 + √5)/2 et Ψ = (1 – √5)/2.
Le nombre Φ est appelé le nombre d’or. Soit f la fonction polynôme du second degré définie sur R par l’expression :
f(x) = x2 – x – 1.
1) Montrer que Φ et Ψ sont les antécédent de 0 par f.
2) En déduire la forme factorisé de f en fonction de Φ et Ψ.
3) Démontrer que, pour tout réel x, on a :
f(x) = (x – 1/2)2 – (5/4).
4) Comment appelle-t-on la forme de l’expression de la question précédente ? C’est la forme ……………. .
5) Dresser le tableau de variation de f sur R.
6) Démontrer que Ψ = 1 – Φ et que Φ = 1 + 1/Φ.
Partie indépendante :
Lors de ces vacances sur la côte bretonne, Miguel veut essayer de sauter dans la mer directement depuis le sommet d’une falaise. Miguel souhaite sauter suffisamment loin pour que l’eau soit assez profonde pour ne pas se blesser. Il estime que pour sauter sans danger, il doit être sûr de toucher la surface de l’eau à + de 10 m du bord de la falaise.
Comme Miguel fera une chute libre avec de négligeables frottements de l’air, son frère Juan lui conseille d’utiliser une fonction du second degré g qui lui permettra de calculer la hauteur, en mètres, de son saut par rapport au niveau de la mer en fonction de la distance horizontale x parcourue, en mètres.
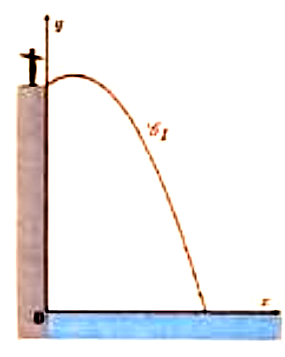
7) En sachant que la falaise a une hauteur de 15 m et que Miguel estime qu’il sera au + haut de son saut à 2 m du bord et qu’il aura alors une altitude de 16.2 m, déterminer l’expression de la fonction g qui lui permettra d’estimer sa trajectoire.
8) À quelle distance de la falaise, Miguel touchera-t-il la surface de l’eau ? Peut-il fait ce saut sans danger ?
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, nombre, or, première.
Exercice précédent : Dérivation – Équation, tangente, point d’abscisse, courbe – Première

