Maths : exercice d’équation de tangente de première et dérivation. Points d’abscisse à trouver, polynômes, courbes, trajectoires, distance.
Exercice N°798 :

Exercice N°798 :
Un train roule sur une voie qui suit un arc de la courbe d’équation
y = x2 avec les distances en kilomètres. Comme l’indique le schéma ci-dessous, une route est matérialisée par l’axe des abscisses.
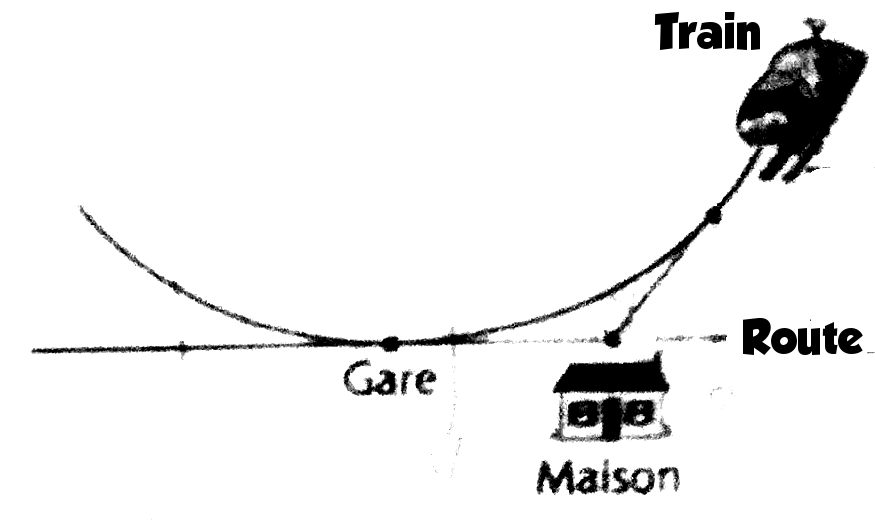
Une gare est située au point de contact entre la voie de chemin de fer et la route asphaltée. Une maison est située au bord de la route à 1 km à l’Est de la gare. Quand le train est en approche de la gare, ses phares éclairent en direction de la maison.
1) Si on note a, l’abscisse du point où se situe le train, quelle est l’équation de la tangente en ce point du train ? On cherche une égalité de type y en fonction de x et de a.
2) Comme cette tangente suit le rayon lumineux rectiligne des phares du train vers la maison, quelle égalité peut-on déduire de l’équation de tangente au niveau de la maison ?
3) Que vaut l’abscisse a ?
4) À quelle distance de la maison le train se trouve-t-il quand il éclaire celle-ci ?
Partie indépendante :
Lors d’une course de Rallycross, un pilote nommé Mathieu a fait une sortie de piste lors du dernier virage en épingle. Il suivait une trajectoire que l’on pourra modéliser par la courbe Cg d’une fonction g définie sur R donc l’expression est :
g(x) = (1/4)x2 + 2x – (5/2).
Alors que Mathieu suivait cette trajectoire Cg, la direction de sa voiture a lâché et il est sorti de la piste en suivant une trajectoire rectiligne correspondant à une tangente à la courbe Cg.
En sachant que sa voiture a percuté le bord du circuit au point A(12 ; 17), on va chercher à déterminer l’endroit précis où s’est produite la panne.
5) Déterminer l’expression de g ‘(x).
6) Si on note b, l’abscisse du point où s’est produite la panne, quelle est l’équation de la tangente en ce point ? On cherche une égalité de type y en fonction de x et de b.
7) Comme cette dernière tangente suit la trajectoire rectiligne de la voiture vers le bord du circuit, quelle égalité peut-on déduire de l’équation de tangente au niveau du point A(12 ; 17) ?
8) Déterminer les abscisses b possibles et les points associés sur la courbe-trajectoire.
9) En sachant que la voiture se déplace vers les x croissants, en déduire les coordonnées exactes du point où a eu lieu l’incident.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, équation, tangente, première.
Exercice précédent : Dérivation – Trouver coefficients d’un polynôme, équations – Première

