Maths de seconde : exercice de quotients avec inéquations, inégalités, démonstration, égalité, maximum, variation, fonction, tableau de signe.
Exercice N°392 :
1) Démontrer l’égalité
(-2x² – 4x + 4)/(2x + 3) = 1 – x – (3x – 1)/(2x + 3).
Soit f définie sur R par
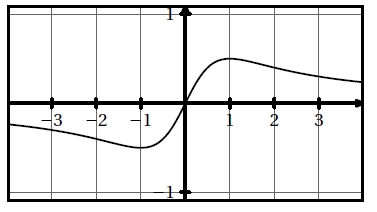
f(x) = x/(x² + 1).
La représentation graphique de f est là-haut.
2) Montrer par calcul que 1/2 est le maximum de f sur R.
3) On sait que x ≥ 0. Comparer alors 1/(x + 1) et 1/(x + 4).
4) On sait que x ≤ 0. Comparer alors 1/(x – 5) et 1/(x – √10).
5) Résoudre (-x + 4)/(2x – 1) ≤ 0.
6) En déduire les solutions de (x + 3)/(2x – 1) ≤ 1.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, quotients, inéquations, inégalités.
Exercice précédent : Quotients – Inéquation, domaine de définition, démonstration – Seconde

