Maths de terminale : exercice de primitive avec encadrement, intégrale. Exponentielle, fraction, carré, encadrement, inégalité, égalité.
Exercice N°426 :

Exercice N°426 :
On se propose de déterminer une valeur approchée à 10-2 de l’intégrale
L = ∫[de 0 à 1] f(x)dx
où f est la fonction définie sur [0 ; 1] par
f(x) = e-x/(2 – x)
1) Démontrer que pour tout x ∈ [0 ; 1],
1/e ≤ f(x) ≤ 1/2
Soit J et K les intégrales définies par :
J = ∫[de 0 à 1] (2 + x)e-xdx
K = ∫[de 0 à 1] x2f(x)dx
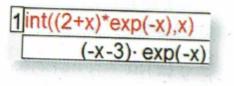
2) Montrer que J = 3 – 4e-1 à l’aide de l’information ci-dessus venant du résultat d’un logiciel de calcul formel.
3) Utiliser l’encadrement 1) pour démontrer que :
1/(3e) ≤ K ≤ 1/6
4) Démontrer que J + K = 4L.
5) En déduire un encadrement de L,
puis donner une valeur approchée de L à 2×10-2 près.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, primitive, encadrement, intégrale.
Exercice précédent : Primitives – Exponentielle, cosinus, rationnelle, limite – Terminale

