Maths : exercice, matrice, inverse, terminale. Fonctions, système d’équations, équation matricielle, colonne, inverse, coefficients.
Exercice N°464 :
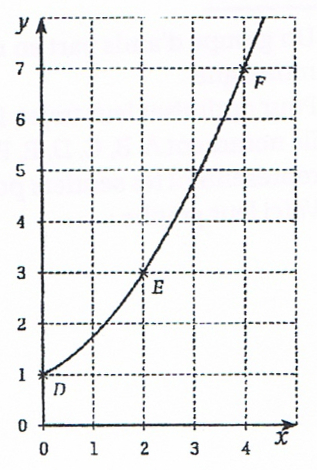
Stéphanie a lancé un réseau d’agence de location de vélos en Bretagne. Depuis 2022, le nombre d’agences n’a fait qu’augmenter. Ainsi on comptait 10 agences au 1er janvier 2022, puis 30 au 1er janvier 2024 et enfin 70 au 1er janvier 2026.
On admet que l’évolution du nombres d’agences peut être modélisée par une fonction f définie sur [0 ; +∞[ par
f(x) = ax2 + bx + c
où a, b et c sont trois nombres réels.
La variable x désigne le nombre d’années écoulées depuis 2022 et f(x) exprime le nombre d’agence en dizaines, la valeur 0 de x correspond donc à l’année 2022. Sur le dessin ci-dessus, on a représenté graphiquement la fonction f.
On cherche à déterminer la valeur des coefficients a, b et c.
1) A partir des données de l’énoncé, écrire un système d’équations S traduisant cette situation.
2) En déduire que le système précédent est équivalent à :
MX = R
avec M =
( 0 0 1 )
( 4 2 1 )
( 16 4 1 ),
X =
( a )
( b )
( c ),
et R une matrice colonne que l’on précisera.
On admet que M-1 =
( 0.125 -0.25 0.125 )
( -0.75 1 -0.25 )
( 1 0 0 )
3) A l’aide de cette matrice, déterminer les valeurs des coefficients a, b et c en détaillant les calculs.
4) Suivant ce modèle, déterminer le nombre d’agences que l’entreprise possédera au 1er janvier 2028.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, matrice inverse, terminale.
Exercice précédent : Primitives – ROC, suite, exponentielle, égalités – Terminale


1) D’après les données, on sait que :
f(0) = 1 car il y a 1 dizaine à l’année (2012 + 0),
f(2) = 3 car il y a 3 dizaines à l’année (2012 + 2),
f(4) = 7 car il y a 7 dizaines à l’année (2012 + 4).
D’après la formule f(x) = ax² + bx + c, on a :
f(0) = a*0² + b*0 + c = 0a + 0b + 1c,
f(2) = a*2² + b*2 + c = 4a + 2b + 1c,
f(4) = a*4² + b*4 + c = 16a + 4b + 1c.
En rassemblant les deux écritures différentes de f(0)=f(0), f(2)=f(2) et f(4)=f(4) ensemble, on obtient le système :
{ 0a + 0b + 1c = 1,
{ 4a + 2b + 1c = 3,
{ 16a + 4b + 1c = 7.
(avec une grande accolade au lieu de trois petites).
2) On reconnait avec 0,0,1 puis 4,2,1 puis 16,4,1 les coefficients de la matrice M.
La partie gauche du système s’écrit donc M*X avec X la matrice colonne aux coefficients a,b,c.
La partie droite sera R, la matrice colonne :
( 1 )
( 3 )
( 7 ).
On a donc MX = R.
3) Pour trouver la matrice X, il faut mettre la matrice inverse de M devant chaque membre de l’égalité :
M-1MX = M-1R
I3X = M-1R (car une matrice fois son inverse fait l’identité).
X = M-1R (car l’identité fois une matrice, donne la même matrice).
Maintenant, il faut faire le produit M-1 et R.

On obtient X =
( 0.25 )
( 0.5 )
( 1 ).
Donc f(x) = 0,25x2 + 0,5x + 1.
En 2018, x = 6, donc f(6) = 0.25*36 + 0.5*6 + 1
= 9 + 3 + 1 = 13 agences.