Maths de terminale : exercice avec limites sur logarithme népérien. Limites, dérivée, variations, courbe, position relative.
Exercice N°360 :
Le plan est rapporté à un repère orthonormal (O ; →i ; →j).
On considère la fonction f définie sur l’intervalle ]0 ; +∞[ par
f(x) = (ln x)/x.
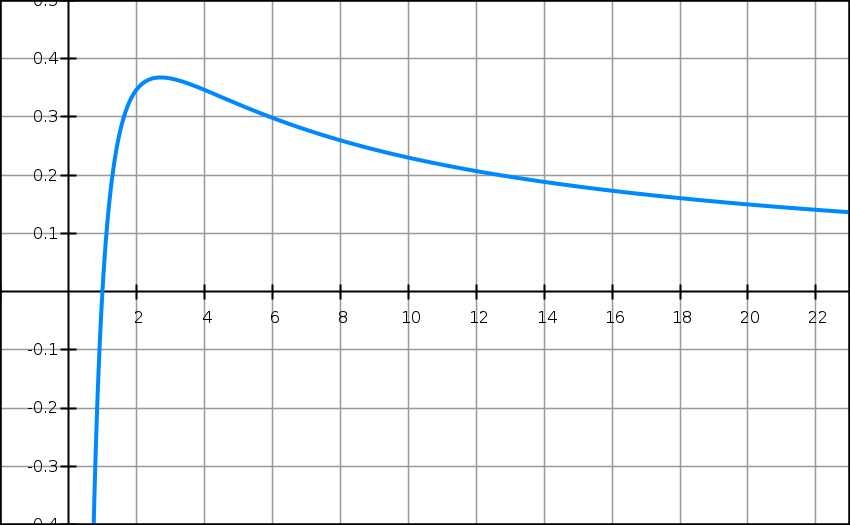
On note f ‘ la fonction dérivée de la fonction f sur l’intervalle ]0 ; +∞[. On note Cf la courbe représentative de la fonction f dans le repère. La courbe Cf est représentée ci-dessus.
1) Déterminer les limites de la fonction f en 0 et en +∞.
2) Calculer la dérivée f ‘ de la fonction f.
3) En déduire les variations de la fonction f.
On considère la fonction g définie sur l’intervalle ]0 ; +∞[ par
g(x)= (ln x)2/x.
On note Cg la courbe représentative de la fonction g dans le repère (O ; →i ; →j).
4) Déterminer la limite de g en 0, puis en +∞. Justifier d’abord la relation :
(ln x)2/x = 4(ln √x)2/(√x)2.
5) Calculer la dérivée g ‘ de la fonction g.
6) Dresser le tableau de variations de la fonction g.
7) Démontrer que les courbes Cf et Cg possèdent deux points communs dont on déterminera les coordonnées.
8) Étudier la position relative des courbes Cf et Cg.
9) Tracer sur le graphique la courbe Cg.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, limites, logarithme, népérien.
Exercice précédent : Logarithme Népérien – Fonctions, exponentielle, suite – Terminale

