Maths de première, exercice de dérivée avec fonction rationnelle. Calculs d’image et de nombre dérivé, courbes et tableau de variation.
Exercice N°286 :
On a tracé ci-dessus, la courbe représentative Cf d’une fonction f définie sur l’intervalle ]−2 ; +∞[. On note f ‘ la dérivée de la fonction f.
1) Par lecture graphique, donner les valeurs de f(1) et de f ‘ (1). Lis la suite »
Exercice de maths de première sur le taux de variation, nombre dérivé, ensemble de dérivabilité, tableau de variations, tangentes.
Exercice N°050 :
Exercice N°050 :
1-2) Des nombres dérivés
Soit f la fonction définie sur R par
f(x) = 1 – x2.
1) Montrer que f est dérivable en a = 2 et calculer f ‘ (2). Lis la suite »
Exercices, dérivées, position relative, maths, terminale, fonction, tableau de signes, position relative, variations, polynôme et racine.
Exercice N°399 :
Exercice N°399 :
Soient f et g les fonctions définies par
f(x) = x2
et
g(x) = x
pour x ∈ R.
On note Pf la parabole représentative de f et D la droite représentative de g dans un repère orthonormé.
1) Dresser le tableau de signes de f(x) − g(x) pour x ∈ R. Lis la suite »
Maths : exercice d’exponentielle avec algorithme de terminale. Fonction, variation, limite, équation, tangente, position relative, continuité
Exercice N°279 :
On considère la fonction f définie sur R par
f(x) = e−x + x.
On note C sa courbe représentative dans un repère orthonormal.
1) Calculer les limites de f en +∞ et −∞.
Au voisinage de −∞, on pourra démontrer que
f(x) = e−x (1 + xex). Lis la suite »
Maths sur les fonctions avec un polynôme, exercice, convexité, terminale, coût, fixe, marginal, point d’inflexion, lecture graphique.
Exercice N°407 :
Dans une entreprise, le coût total, en euros, pour la fabrication de machines est modélisé par la fonction définie sur l’intervalle [0 ; 100] par l’expression :
C(q)= 0.05q3 – 6q2 + 400q + 1000.
La fonction C est représentée par la courbe ci-dessus dans un repère orthogonal.
1) Quels sont les coûts fixes de production ? Lis la suite »
Exercice de maths de terminale de fonction avec courbe, équation réduite, point d’inflexion, tangente, graphique, variation, bénéfice.
Exercice N°404 :
On donne ci-dessus la représentation graphique de la fonction f définie sur [0,5 ; 10] et on note Cf la représentation graphique de la fonction f.
T, T ‘ et T ‘ ‘ sont les tangentes à la courbe au points A d’abscisse 1 et B d’abscisse 4 et C d’abscisse 3/2.
Partie A – En utilisant le graphique :
1) Déterminer f ‘ (1) et donner une valeur approchée aux dixièmes de f ‘ (4). Lis la suite »
Maths de terminale sur les fonctions. Exercice sur un bénéfice, polynôme, rationnelle, droite, coût, quantité, graphique, maximum, dérivée.
Exercice N°403 :
L’entreprise Sheddi produit du tissu en coton. Celui-ci est fabriqué en 1 mètre de large et pour une longueur x exprimée en kilomètre, x étant compris entre 0 et 10.
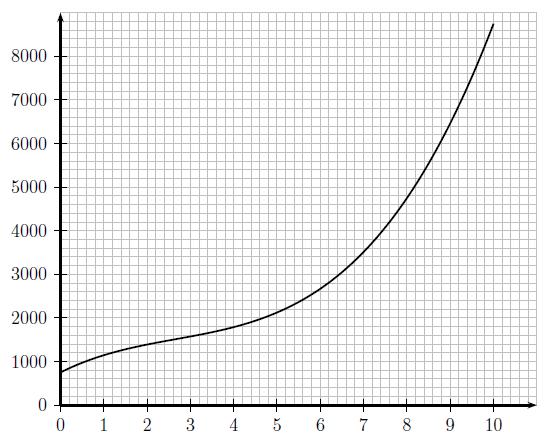
Le coût total de production en euros de l’entreprise Sheddi est donné en fonction de la longueur x par la formule
C(x) = 15x3 − 120x2 + 500x + 750.
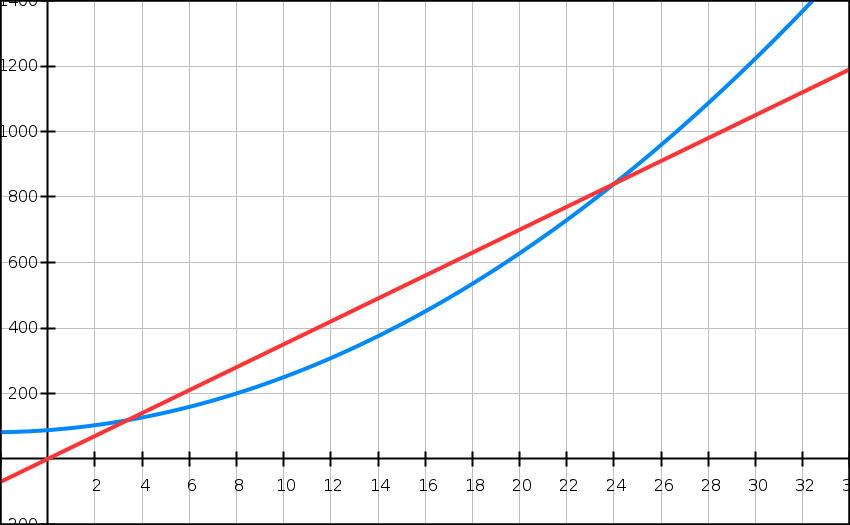
Le graphique ci-dessus donne la représentation graphique de la fonction C.
Les deux parties A et B de cet exercice sont indépendantes.
Partie A : Étude du bénéfice
Si le marché offre un prix p en euros pour un kilomètre de ce tissu, alors la recette de l’entreprise Sheddi pour la vente d’une quantité x est égal à
R(x) = px.
1) Tracer sur le graphique la droite D1 d’équation
y = 400x.
Expliquer, au vu de ce tracé, pourquoi l’entreprise Sheddi ne peut pas réaliser un bénéfice si le prix p du marché est égal à 400 euros. Lis la suite »
Maths de première, exercice avec lecture graphique et fonction. Second degré et affine, lecture graphique, coût, recette, bénéfice, tableau.
Exercice N°318 :
Exercice N°318 :
Le comptable d’une usine chimique estime que, pour fabriquer q hectolitres d’un certain produit, avec q compris entre 0 et 30, le coût total en centaines d’euros est donné par la fonction C représentée ci-dessous.
On suppose que toute la production est vendue. La recette, en centaines d’euros, réalisée par la vente de q hectolitres de ce produit est donnée par la fonction R représentée ci-dessus par un segment de droite.
1) Recopier et compléter le tableau suivant à l’aide du graphique. Lis la suite »
Exercice de maths de seconde avec l’aire d’un quadrilatère, calcul de géométrie, surfaces de triangles, équations du second degré.
Exercice N°040 :
Soit ABCD un rectangle tel que AB = 7 cm et BC = 5 cm. Le point M appartenant à [AB] est défini par AM = a avec 0 < a <5.
On place de même les points N, P et Q tels que AM = BN = CP = DQ (voir figure).
On veut calculer l’aire X de la surface coloriée MNPQ.
1) Rappeler l’expression de l’aire d’un triangle EFG rectangle en E. Lis la suite »
Maths de première : exercice d’équations du second degré. Factorisation, identités remarquables, discriminant, delta, solutions.
Exercice N°262 :
Exercice N°262 :
1-8) Résoudre les équations suivantes :
1) 4x² – 9 = 0, Lis la suite »
