Exercice sur les vecteurs avec parallélogramme de première. Maths, relations vectorielles, appartenance à une droite, colinéarité, égalités.
Exercice N°597 :

Exercice N°597 :
ABCD est un parallélogramme. Les points I et K sont les milieux respectifs de [AB] et [CD].
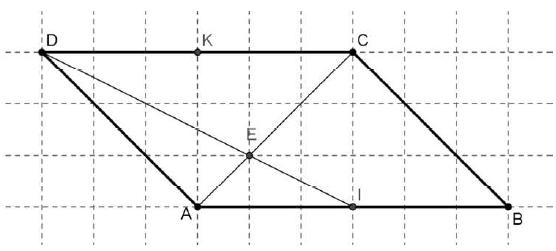
1) Exprimer le vecteur →DI en fonction de →AB et →AD.
2) Soit E le point défini par →DE = (2/3)→DI.
3) Exprimer le vecteur →AE en fonction de →AB et →AD.
4) En déduire que →AE = (1/3)→AC.
5) Que peut-on dire des points A, E et C ?
Soit F le symétrique de A par rapport à E.
6) Exprimer le vecteur →AF en fonction de →AC.
7) Exprimer le vecteur →AF en fonction de →AB et →AD.
8) Exprimer le vecteur →BK en fonction de →AB et →AD.
9) Démontrer que F appartient à la droite (BK).
Bon courage,
Sylvain Jeuland
Pour avoir le corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de Terminale de ce chapitre (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés de l’exercice : exercice, vecteurs, parallélogramme, première.
Exercice précédent : Vecteurs – Triangles, relations, égalités, alignés – Première

