Maths de première : exercice, vecteurs, points alignés, égalités et relations vectorielles. Triangle, points alignés, parallélisme, dessin.
Exercice N°596 :

Exercice N°596 :
Soit un triangle SRT et K le milieu de [RS].
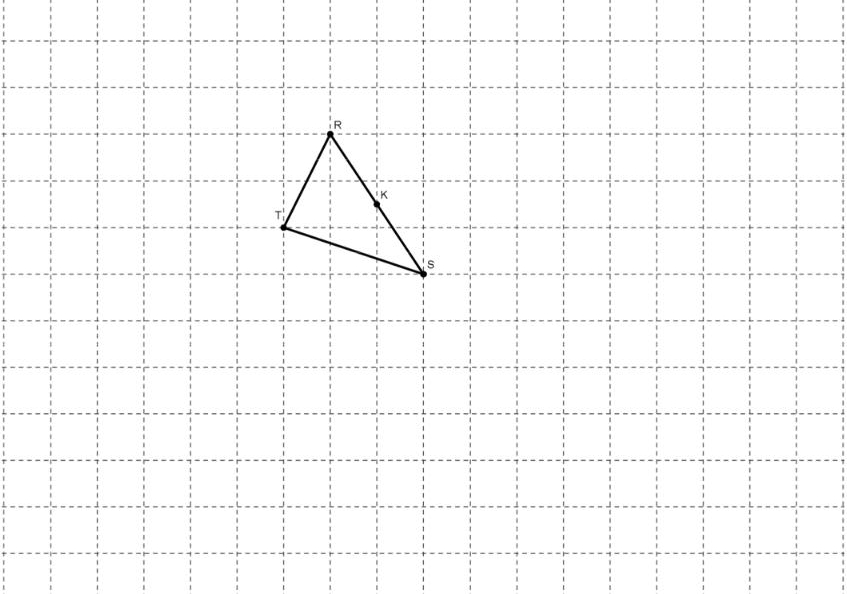
1) Construire sur la figure ci-dessus les point H et L tels que :
→TH = -3→TR et
→SL = -2ST
2) Montrer que
→TR + →TS = 2→TK.
3) Exprimer →HL en fonction de →TR et →TS.
4) En déduire que les droites (HL) et (TK) sont parallèles.
On considère le point A défini par
2→SA – 2→TA + →AR = →0.
5) Montrer que
→SA = 2→ST + →SR.
6) Montrer que les points A, K et L sont alignés.
Questions indépendantes avec des triangles et des théorèmes :
Étant donné un triangle EFG, on pose I et J les milieux respectifs de [EF] et [EG].
7) Démontrer que →IJ = (1/2)→FG, c’est-à-dire la version vectorielle du théorème de la droite des milieux.
Dans le triangle MNO, on pose P et Q tels que :
→MP = k→MN
et
→MQ = k→MO
avec k un nombre réel quelconque.
8) Démontrer que →PQ = k→NO, c’est-à-dire la version vectorielle de la réciproque du Théorème de Thalès.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, vecteurs, points alignés.
Exercice précédent : Statistiques – Séries, comparaisons, diagrammes, boîtes – Première

