Exercice de maths de terminale sur qcm, primitives et intégrales avec études de courbes, pente, tangente, aire sous la courbe
Exercice N°470 :

Exercice N°470 :
QCM avec une seule bonne réponse possible par question :
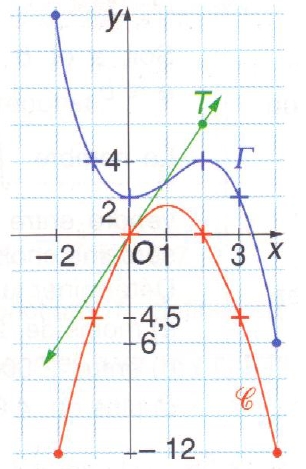
Pour les questions 1) à 6), on considère la fonction f définie et dérivable sur
[-2 ; 4] représentée par la courbe C et la g fonction définie et dérivable sur
[-2 ; 4] représentée par la courbe Γ Les points notés par une croix sont des
points connus de ces courbes. La droite T est la tangente à la courbe C de au
point d’abscisse 0.
1) Laquelle de ces phrases est vraie ?
a) f est une primitive de g,
b) g est une primitive de f,
c) g est la dérivée de f.
2) f ‘ (0) = :
a) 0,
b) 3,
c) 3/2.
3) Le coefficient directeur de la tangente à la courbe de g au point d’abscisse 3 est :
a) -4.5,
b) 2,
c) On en peut pas répondre.
4) Les solutions de f ‘ (x) > 0 sont :
a) S = [-2 ; 1[,
b) S = ]0 ; 2[,
c) S = ]-2 ; 1[,
5) ∫[de 0 à 2] f(x) dx = :
a) 1,
b) 2,
c) 3.
6) Laquelle de ces intégrales se traduit par une aire ?
a) ∫[de 1 à 2] f(x) dx,
b) ∫[de 0 à 3] f(x) dx,
c) ∫[de 2 à 4] f(x) dx.
7) On sait que ∫[de 1 à 3] h(x) dx = 2.
Alors ∫[de 1 à 3] [4h(t) – t] dt = :
a) 4,
b) 3,
c) 6.
Bon courage,
Sylvain Jeuland
Pour avoir le corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de Terminale de ce chapitre (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés de l’exercice : qcm, primitives, intégrales, terminale.
Exercice précédent : Primitives – Intégrale, moyenne, aires, puissance – Terminale

