Exercice de maths de terminalede géométrie dans l’espace avec section. Vecteur normal, équation, plan, sphère, cercle, projeté.
Exercice N°485 :
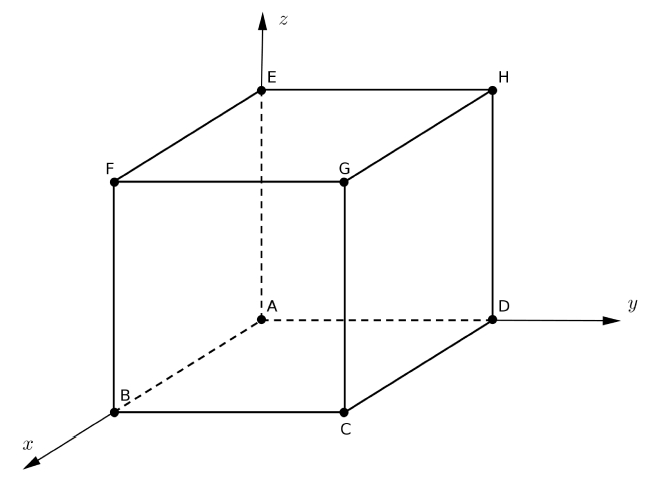
On considère le cube ABCDEFGH représenté ci-dessus. L’espace est rapporté au repère orthonormal (A ; →AB ; →AD ; →AE).
On désigne par I, J et K les milieux respectifs des segments [BC], [BF] et [HF].
1) Déterminer les coordonnées des points I, J et K.
2) Démontrer que le vecteur →n(2 ; 1 ; 1) est orthogonal à →IK et à →IJ.
3) En déduire qu’une équation du plan (IJK) est :
4x + 2y + 2z − 5 = 0.
4) Déterminer un système d’équations paramétriques de la droite (CD).
5) En déduire que le point d’intersection R du plan (IJK) et de la droite (CD) est le point de coordonnées (3/4 ; 1 ; 0). Placer le point R sur la figure.
6) Tracer sur la figure la section du cube par le plan (IJK). On peut répondre à cette question sans avoir traité les précédentes.
7) Montrer que que le point T, projeté orthogonal de G sur (IJK) a pour coordonnées (1/2 ; 3/4 ; 3/4).
8) Montrer que la distance du point G au plan (IJK) est √6/4.
9) Soit S la sphère de centre G passant par F. Justifier que la sphère S et le plan (IJK) sont sécants.
10) Déterminer le rayon du cercle d’intersection de S et (IJK).
11) Construire l’intersection de (IJK) et (EDG). Justifier la construction.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : géométrie dans espace, section.
Exercice précédent : Géométrie Espace – Vecteur normal, cartésienne, sphère – Terminale

