Maths de première : exercice sur les probabilités conditionnelles avec tableau, arbre pondéré, sachant, intersection, calculs, formules.
Exercice N°804 :

Exercice N°804 :
Le tableau ci-dessous donne la répartition des trois formules choisies par les 600 adhérents d’un club de remise en forme : formule sportive (S), formule relaxation (R) et formule liberté (L) qui donne accès à toutes les installations.
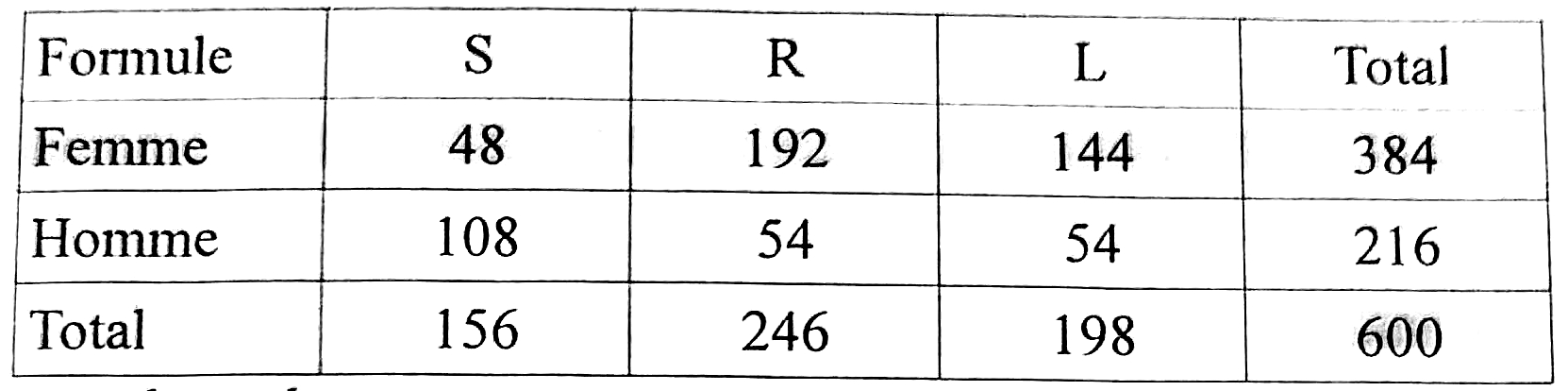
On choisit un adhérent au hasard.
On considère les événements suivants :
F : “L’adhérent est une femme”.
S : “L’adhérent a choisi la formule sportive”.
R : “L’adhérent a choisi la formule relaxation”.
L : “L’adhérent a choisi la formule liberté”.
1) Calculer la probabilité que l’adhérent soit une femme.
2) Calculer la probabilité que l’adhérent soit un homme et qu’il ait choisi la formule sportive.
3) Calculer la probabilité que l’adhérent soit un femme sachant qu’il a choisi la formule liberté.
Partie indépendante :
Une enquête réalisée auprès des candidats qui passent l’épreuve du Code de la Route montre que 75 % d’entre eux déclarent avoir préparé sérieusement cette épreuve. Lorsque c’est le cas, le candidat obtient le code dans 80% des cas. Si l’épreuve n’est pas bien préparée, le candidat obtient le code dans 40% des cas.
On choisit au hasard un candidat à l’issue de l’épreuve.
On considère les événements suivants :
T : “Le candidat a travaillé sérieusement pour préparer l’épreuve”.
C : “Le candidat a réussi l’épreuve et a obtenu son code”.
4) Construire un arbre pondéré traduisant la situation.
5) Calculer la probabilité que le candidat ait travaillé sérieusement pour préparer l’épreuve et l’ait réussie et obtenu son code.
6) Calculer la probabilité que le candidat ait réussi l’épreuve et obtenu son code.
7) Calculer la probabilité que le candidat ait travaillé sérieusement pour préparer l’épreuve sachant qu’il l’a réussie et a obtenu son code.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, probabilités conditionnelles, tableau.
Exercice précédent : Trigonométrie – Polynôme, équations, sinus, cosinus – Première

