Exercice de matrice adjacente de terminale avec graphe. Degrés, arêtes, sommets, chemins, chaîne eulérienne, nombre.
Exercice N°467 :
Voici le plan d’un musée : les parties grisées matérialisent les portes et les visiteurs partent de l’accueil, visitent le musée et doivent terminer leur visite à la boutique.
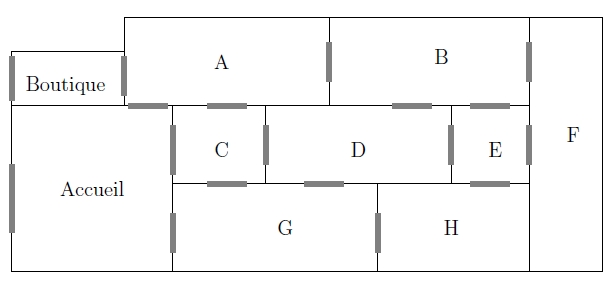
1) Représenter la situation à l’aide d’un graphe en précisant ce que représentent arêtes et sommets.
2) Pourquoi est-il possible de trouver un circuit où les visiteurs passent une fois et une seule par toutes les portes ?
3) Les visiteurs, en entrant dans chaque salle, reçoivent une plaquette de présentation de la salle, quel est le nombre minimum de plaquettes qu’ils auront en main en arrivant à la boutique, s’ils ont suivi un circuit dans lequel ils sont passés une fois et une seule par toutes les portes ?
4) Donner un exemple d’un tel circuit.
On note G2 le sous-graphe obtenu en supprimant la boutique et l’accueil.
5) Écrire la matrice d’adjacence M du sous-graphe G2(en ordonnant les sommets dans l’ordre alphabétique de A à H).
On donne les matrices M2 et M3 :


Un visiteur est actuellement dans la salle B, on lui signale qu’il a laissé un sac dans la salle E ; devant le récupérer, il souhaite passer au maximum par trois portes.
6) Indiquer le nombre de possibilités, en utilisant les matrices.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, matrice, adjacente, terminale.
Exercice précédent : Graphes – Degré, chaîne eulérienne, nombre chromatique – Terminale

