frenchmaths.com (par Sylvain Jeuland)

Maths de première : exercice d’applications du produit scalaire, ensemble de points, tangente, cercle, relation de Chasles, triangle.

Exercice N°808 :

Exercice N°808 :

Le plan est muni d’un repère orthonormé.
C₁ est le cercle de centre A(0 ; −1.5) passant par le point B(−2 ; 1).
C₂ est le cercle de centre C(3.25 ;−3) passant par le point D(7 ; 0).

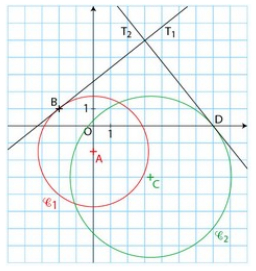
1) Démontrer que la tangente T₁ en B au cercle C₁ est perpendiculaire à la tangente T₂ en D au cercle C₂.

2-3) EFG est un triangle. I est le milieu du côté [FG].

2) En utilisant la relation de Chasles avec ^→EF et ^→EG, démontrer que :
EF² + EG² = 2EI + (¹/₂)FG².

On suppose que : EF = 4 cm, EG = 5 cm et FG = 6 cm.
3) Calculer la longueur EI en cm en arrondissant au dixième.

4-5-6) On considère les points K(-2 ; -3) et L(-1 ; 4).

4) Calculer la longueur KL.

5) Déterminer les coordonnées de J, le milieu du segment [KL].

6) Déterminer l’ensemble des points M du plan vérifiant :
^→MK.^→ML = 0.

On donne les points R et S tel que RS = 10 et H le milieu du segment [RS].
7) Déterminer l’ensemble des points N du plan vérifiant :
^→NR.^→NS = -9.

Bon courage,
Sylvain Jeuland

Mots-clés de l’exercice : exercice, applications, produit scalaire.

Exercice précédent : Produits scalaires – Cosinus, norme, angle, coordonnées – Première