Exercice de maths avec raisonnement par récurrence de terminale. Suite, algorithme, boucle tant que, calculs, analyse de données.
Exercice N°165 :
On considère l’algorithme suivant (N désigne un entier naturel) :
1) Pourquoi cet algorithme s’arrête ? Lis la suite »
Maths de terminale : exercice d’algorithme avec somme de suite. Boucle tant que, condition, affectations, variables, entrées, sortie.
Exercice N°164 :
On donne l’algorithme ci-dessus.
1) Que fait cet algorithme ? Lis la suite »
Maths : exercice d’exponentielle avec algorithme de terminale. Fonction, variation, limite, équation, tangente, position relative, continuité
Exercice N°279 :
On considère la fonction f définie sur R par
f(x) = e−x + x.
On note C sa courbe représentative dans un repère orthonormal.
1) Calculer les limites de f en +∞ et −∞.
Au voisinage de −∞, on pourra démontrer que
f(x) = e−x (1 + xex). Lis la suite »
Maths de terminale : exercice de suite géométrique avec algorithme, arithmétique, somme de termes, formule explicite, calculatrice, calculs.
Exercice N°230 :
Exercice N°230 :
Une entreprise fabriquant des tables en bois souhaite se développer rapidement et veut planifier l’augmentation de sa production chaque année.
En 2051, 3000 tables par an ont été fabriquées.
Deux options sont possibles pour augmenter la production :
– Plan 1: on augmente la production annuelle de 180 tables chaque année.
– Plan 2 : on augmente la production de 5 % par an.
On note un le nombre de tables fabriquées pendant l’année (2051 + n) avec le plan 1.
1) Déterminer u0. Lis la suite »
Maths de seconde : exercice de second degré et d’algorithme. Fonction, équation (graphique, calcul). Courbe, repère, symétrie, factorisation.
Exercice N°018 :
Dans cet exercice, chaque partie peut-être traitée indépendamment des autres.
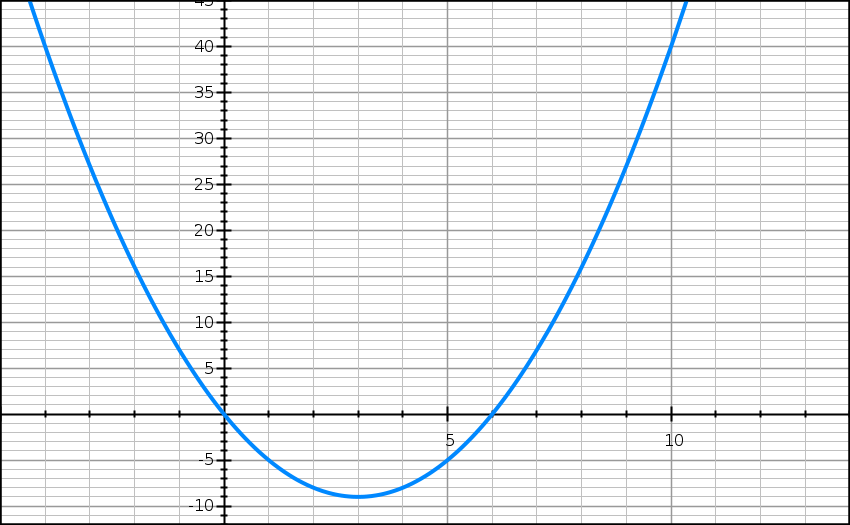
On considère, dans tout l’exercice, la fonction f définie sur R par
f(x) = (x – 3)2 – 9,
et la fonction g définie sur R par
g(x) = -(x – 6)2 + 36.
Leurs courbes représentatives respectives seront notées Cf et Cg.
Partie A : un peu d’algorithmique :
On considère l’algorithme suivant :
1) Comment compléter l’algorithme précédent de sorte que si l’utilisateur entre une valeur x, l’algorithme affiche l’image de x par g. Lis la suite »
Exercice de maths de terminale : algorithme, suite géométrique, boucle tant que. Variable, initialisation, condition, traitement, raison.
Exercice N°186 :
Voici un algorithme :
1) Que fait cet algorithme ? Lis la suite »
Exercice de maths de terminale avec algorithme, graphique, suite arithmétique, fonction, raisonnement par récurrence, limite.
Exercice N°173 :
On considère la suite (un) définie pour tout n ∈ N par
u0 = -2 et, pour tout entier n,
un+1 = un/(1 – un).
On admet pour commencer que pour tout entier naturel n,
un ≠ 1.
1) Calculer u1 et u2. Lis la suite »
Maths de terminale : exercice de suite avec fonction, algorithme. Tableau de variation, limite, raisonnement par récurrence, démonstration.
Exercice N°168 :
L’objet de cet exercice est d’étudier la suite (un) définie sur N par
u0 = 3
et pour tout entier naturel n,
un+1 = 1/2(un + 7/un) (⋆)
On pourra utiliser sans démonstration le fait que pour tout entier naturel n,
un > 0.
On désigne par f la fonction définie sur l’intervalle ]0 ; +∞[ par :
f(x) = (1/2)(x + 7/x) = (1/2)(x² + 7)/x.
1) Établir le tableau de variation de f. Lis la suite »
Maths de seconde : exercice d’algorithme avec entrée, sortie. Fonction de calcul, expression littérale, variable, affectation.
Exercice N°584 :
Exercice N°584 :
L’algorithme suivant transforme la mesure d’une température donnée en degrés Celsius (utilisé en France) en sa mesure en degrés Fahrenheit (utilisé en Angleterre).
Variables C, F : réels
Début
– Afficher (« Entrer la température en degrés Celsius »)
– Entrer (C)
– Affecter à F le résultat de (9/5)×C + 32
– Afficher (« la température en degrés Fahrenheit est : « , F)
Fin
1) Quel est le nombre affiché en sortie si l’entrée est 0 (pour 0° Celsius) ? Lis la suite »
Maths de seconde : exercice d’algorithme, si alors sinon, condition, affectation,variables, stockage, fin si, entrée, sortie..
Exercice N°583 :
Exercice N°583 :
On considère l’algorithme suivant : Lis la suite »
