Maths de seconde sur la géométrie : exercice d’espace avec plans et droites. Cube, parallélisme, sécants, coplanaires, intersections.
Exercice N°267 :
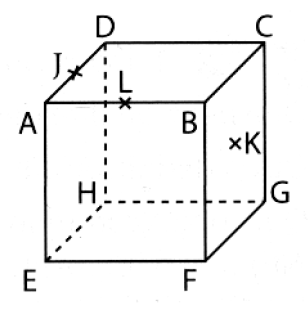
1) Les droites (AB) et (HG) sont-elles parallèles ? Lis la suite »
Maths de seconde : exercice sur la géométrie dans l’espace avec pyramide et pavé. Construction de points, plans, droite, parallélisme.
Exercice N°266 :
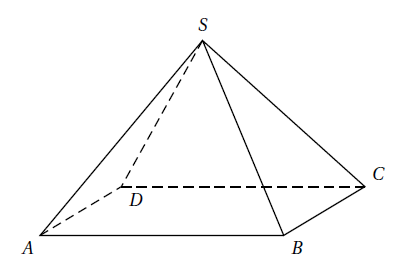
SABCD est une pyramide à base carrée.
I est le point du segment [SB] tel que
→SI = 2/3 →SB.
J est le point du segment [SC] tel que
→SJ = 2/3 →SC.
Le plan (CDI) coupe la droite (SA) en K.
1) Construire les points I et J. Lis la suite »
Géométrie 3D – Pyramide, intersections, plans, patron – Seconde
11 octobre 2020
Exercice de maths de seconde sur la géométrie avec une pyramide, intersection, plans. Parallélépipède rectangle, droites, distances.
Exercice N°265 :
Soit SABCD la pyramide de sommet S représentée ci-contre. Les constructions suivantes sont à faire sur ce dessin :
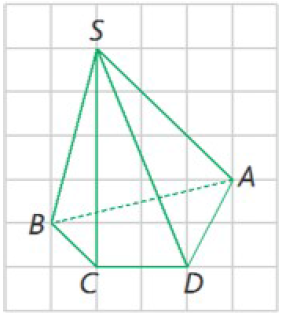
1) Construire le point I, intersection de (BC) et (AD).
2) Déterminer et construire, en rouge, l’intersection des plans (SBC) et (SAD). Lis la suite »
Maths : exercice de géométrie dans l’espace de seconde. Pyramide, tétraèdre, droite d’intersection, plans, parallélisme, milieux, sphère.
Exercice N°264 :
Exercice N°264 :
Soit SABCD une pyramide de sommet S et dont la base ABCD est un rectangle.
1) Faire une figure. Lis la suite »
Vecteurs – Coordonnées, parallélisme, milieu, repères – Première
11 octobre 2020
Exercice avec coordonnées, milieu, vecteur. Maths de première, relations vectorielles, parallélisme, alignement de points, figure.
Exercice N°598 :
Exercice N°598 :
Dans un repère (O ; →i ; →j),
on considère les points R(-2 ; -3), S(3 ; 3) et T(4 ; -1).
1) Calculer les coordonnées du point P défini par
→OP = →OR – →OS + →OT. Lis la suite »
Maths de première, exercice avec lecture graphique et fonction. Second degré et affine, lecture graphique, coût, recette, bénéfice, tableau.
Exercice N°318 :
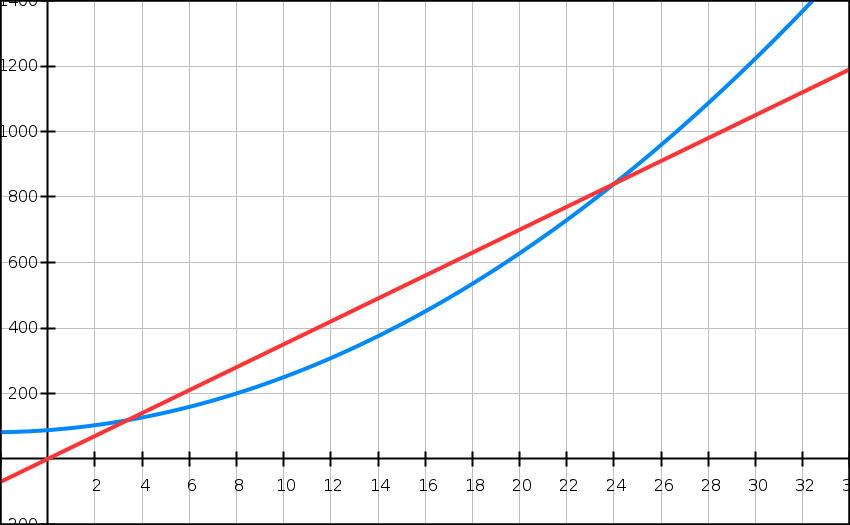
Exercice N°318 :
Le comptable d’une usine chimique estime que, pour fabriquer q hectolitres d’un certain produit, avec q compris entre 0 et 30, le coût total en centaines d’euros est donné par la fonction C représentée ci-dessous.
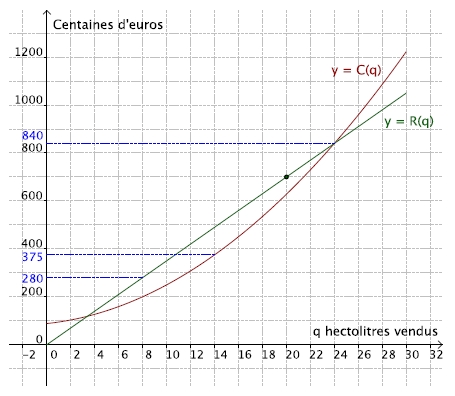
On suppose que toute la production est vendue. La recette, en centaines d’euros, réalisée par la vente de q hectolitres de ce produit est donnée par la fonction R représentée ci-dessus par un segment de droite.
1) Recopier et compléter le tableau suivant à l’aide du graphique. Lis la suite »
Géométrie et Equations – Aire d’un quadrilatère – Seconde
9 octobre 2020
Exercice de maths de seconde avec l’aire d’un quadrilatère, calcul de géométrie, surfaces de triangles, équations du second degré.
Exercice N°040 :
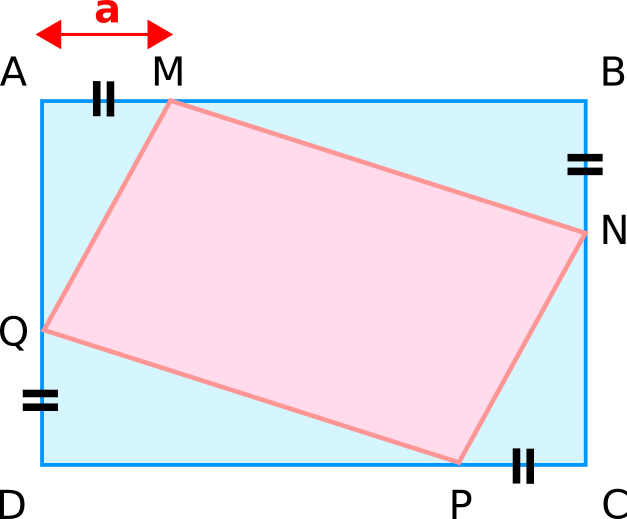
Soit ABCD un rectangle tel que AB = 7 cm et BC = 5 cm. Le point M appartenant à [AB] est défini par AM = a avec 0 < a <5.
On place de même les points N, P et Q tels que AM = BN = CP = DQ (voir figure).
On veut calculer l’aire X de la surface coloriée MNPQ.
1) Rappeler l’expression de l’aire d’un triangle EFG rectangle en E. Lis la suite »
Exercice de maths sur l’intersection et la réunion d’intervalle en seconde avec inégalités, et, ou, appartient, tracer l’axe des abscisses.
Exercice N°648 :
Exercice N°648 :
1-2-3-4) Déterminer et simplifier les ensembles suivants :
1) ] −∞ ; 8 ] ∪ ] −3 ; 10 ] = …………………………… , Lis la suite »
Maths de seconde :contrôle sur intervalle avec réunion et intersection. Appartenance, tracer des axes, symboles, crochets, ouvert, fermé.
Exercice N°647 :
Exercice N°647 :
1-2-3-4-5) Pour chacun des exercices suivants, dire si I∪J est un intervalle. Utiliser la notation usuelle pour écrire I∪J et I∩J.
1) I = ] −∞; −1 [ et J = ] −∞ ; −2/3 ]¸ Lis la suite »
Mots-clés de l’exercice : Maths : exercice, intervalles, inégalités, seconde. Plus grand, plus petit, égal, crochets, axe des abscisses, réels, ensemble de nombre.
Exercice N°575 :
Exercice N°575 :
Pour chaque inégalité, écrire à l’aide d’intervalles les ensembles de réels x vérifiant les inégalités suivantes. Tracer l’axe des abscisses en entourant le ou les bon(s) intervalles(s).
1) L’inégalité est :
x < -2
donc l’intervalle I = ? Lis la suite »
