Exercice de maths de terminale de géométrie 3D, distance, point, droite, espace, plan, équation paramétrique, vecteur normal, directeur.
Exercice N°481 :
Exercice N°481 :
L’espace est rapporté à un repère orthonormé (→i ; →j ; →k).
On considère la droite D passant par le point A de coordonnées (3 ; -4 ; 1) et dont un vecteur directeur est →u(1 ; -3 ; 1).
On considère la droite D ‘ dont une représentation paramétrique est :
{ x = -1 – t
{ y = 2 + t (t ∈ R)
{ z = 1 – t
On admet qu’il existe une unique droite Δ perpendiculaire aux droites D et D ‘. On se propose de déterminer une représentation paramétrique de cette droite Δ et de calculer la distance entre les droites D et D ‘, distance qui sera définie aux questions 8) et 9.
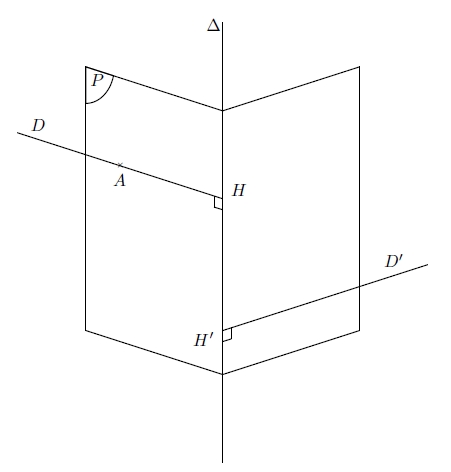
On note H le point d’intersection des droites D et Δ, H ‘ le point d’intersection des droites D ‘ et Δ. On appelle P le plan contenant la droite D et la droite Δ. On admet que le plan P et la droite D ‘ sont sécants en H ‘.
Voici à nouveau la figure :

On considère le vecteur →w de coordonnées (1 ; 0 ; -1).
1) Démontrer que →w est un vecteur directeur de la droite Δ.
Soit →n le vecteur de coordonnées (3 ; 2 ; 3).
2) Démontrer que le vecteur →n est normal au plan P.
3) Montrer qu’une équation cartésienne du plan P est
3x + 2y + 3z – 4 = 0.
4) Démontrer que le point H ‘ a pour coordonnées (-1 ; 2 ; 1).
5) En déduire une représentation paramétrique de la droite Δ.
6) Déterminer les coordonnées du point H.
7) Calculer la longueur HH ‘.
Questions “trace de recherche” :
L’objectif de cette question est de montrer que, pour tout point M appartenant à la droite D et tout point M ‘ appartenant à D ‘, MM ‘ ≥ HH ‘.
8) Montrer que →MM ‘ peut s’écrire comme la somme de →HH ‘ et d’un vecteur orthogonal à →HH ‘.
9) En déduire que ||→MM’||2 ≥ ||→HH’||2 et conclure.
Petite conclusion : La longueur HH ‘ réalise donc le minimum des distances entre un point de D et un point de D ‘. On l’appelle donc la distance entre les droites D et D ‘.
Bon courage,
Sylvain Jeuland
Question 1 : Clic droit vers le corrigé
Pour avoir la suite du corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de ce chapitre (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés de l’exercice : distance, point, droite, espace.
Exercice précédent : Géométrie Espace – Produit scalaire, paramétrique – Terminale

