Maths de terminale : exercice de loi normale, courbe de Gauss, probabilité. Moyenne, espérance, écart-type, surfaces, aires, abscisses.
Exercice N°439 :

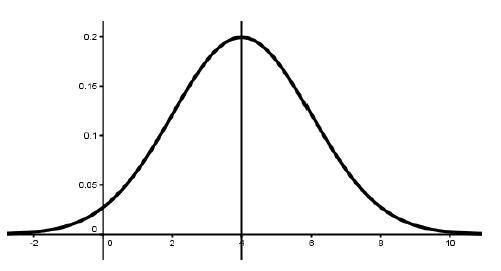
Une variable aléatoire Z suit une loi normale N(m, σ2) avec m = 4 et σ = 2.
1) Donner la valeur des trois probabilités :
P(2 ≤ Z ≤ 6),
P(0 ≤ Z ≤ 8)
et
P(-2 ≤ Z ≤ 10).
On arrondira les résultats à 10-3 près.
2) Donner la valeur du nombre k tel que
P(Z ≤ k) = 0,4.
3) Donner la valeur du nombre l tel que
P(Z ≥ l) = 0,7.
4) Donner la valeur du nombre δ tel que
P(4 – δ ≤ Z ≤ 4 + δ) = 0,5.
5) Placer approximativement les nombres k, l, 4-δ et 4+δ et sur les graphiques ci-dessous et colorier l’aire correspondante.








Une variable aléatoire Y suit une loi normale N(2 ; σ2). On ne connait pas σ mais on sait que :
P(1 ≤ Y ≤ 3) = 0,56.
6) Calculer P(Y ≥ 3) en justifiant.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, loi normale, courbe.
Exercice précédent : Lois continues – Probabilité, uniforme, normale – Terminale

