Exercice sur loi normale de terminale. Maths, probabilités avec courbe de Gauss, écart-type, moyenne, espérance, variable, binomiale
Exercice N°435 :
La variable aléatoire X suit la loi normale d’espérance μ et d’écart type σ. La fonction de densité X correspondante est donnée dans le repère ci-dessous.
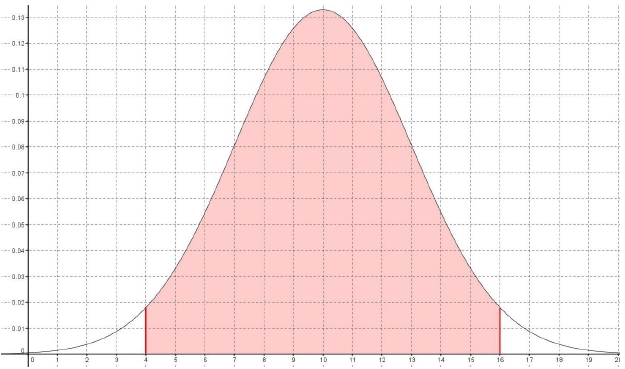
L’aire du domaine limité par la courbe, l’axe des abscisses et les droites d’équations x = 4 et x = 16 est d’environ 0.95 unités d’aire.
1) Déterminer μ par lecture graphique.
2) Donner alors la probabilité P(X ≤ 10).
On rappelle que si la variable aléatoire X suit la loi normale d’espérance μ et d’écart type σ, on a
P(μ – 2σ < X < μ + 2σ) ≃ 0.95.
3) En déduire la valeur de σ.
4) Avec la calculatrice, déterminer alors K, arrondi aux dixièmes,
tel que
P(X ≥ K) = 0,6.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, loi normale, terminale.
Exercice précédent : Lois continues – Densité, uniforme, normale, espérance – Terminale

