Exercice : Clic droit vers l’exercice
Tout le corrigé :
f(x) = (2x + 1)ex
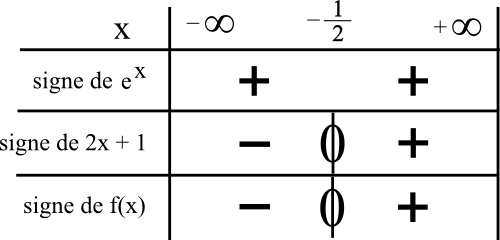
1) Pour déterminer le signe du produit f(x), qui a deux facteurs, on construit un tableau de signe avec chacun des facteurs.
Un exponentiel est toujours strictement positif quelque soit son contenu donc on met un unique + dans la ligne de l’exponentielle.
On met un “+” pour 2x + 1
⇔ 2x + 1 ≥ 0
⇔ 2x ≥ -1
⇔ x ≥ –1/2
⇔ on est à droite de –1/2 dans la première ligne du tableau de signe.
Donc on met le “+” à droite du “0” en dessous de –1/2.
On obtient donc le tableau suivant :
2) Pour déterminer les variations d’une fonction, on détermine d’abord le signe de la fonction dérivée.
f(x) = (2x + 1)ex
= u(x) × v(x)
avec
u(x) = 2x + 1,
u ‘ (x) = 2,
v(x) = ex,
v ‘ (x) = ex.
La dérivée du produit f(x) est donc la formule :
f ‘ (x) = u ‘ (x) × v(x) + u(x) × v ‘ (x)
Du coup, f ‘ (x) = 2×ex + (2x + 1)×ex
= ex × (2 + (2x + 1)) (en factorisant par l’exponentiel)
= ex × (2x + 3)
Pour déterminer le signe du produit f ‘ (x), qui a deux facteurs, on construit un tableau de signe avec chacun des facteurs.
Un exponentiel est toujours strictement positif quelque soit son contenu donc on met un unique + dans la ligne de l’exponentielle.
On met un “+” pour 2x + 3
⇔ 2x + 3 ≥ 0
⇔ 2x ≥ -3
⇔ x ≥ –3/2
⇔ on est à droite de –3/2 dans la première ligne du tableau de signe.
Donc on met le “+” à droite du “0” en dessous de –3/2.
On obtient donc le tableau suivant :
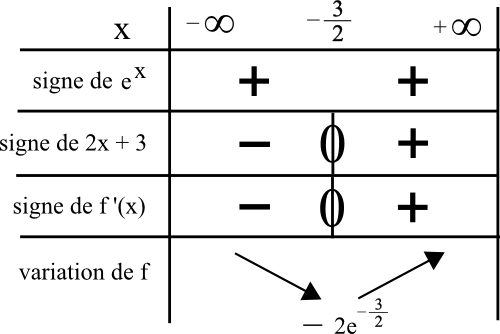
Le minimum est atteint en –3/2.
On calcule f(-3/2) en remplaçant x par –3/2dans l’expression de f(x).
3) Pour déterminer la convexité du fonction f, on fait le tableau de signe de f ‘ ‘ (x).
Voici un exemple ci-dessous qui ne correspond par à l’exercice ici :
Déterminons notre dérivée seconde f ‘ ‘ (x) :
f ‘ (x) = (2x + 3) × ex
= u(x) × v(x)
avec
u(x) = 2x + 3,
u ‘ (x) = 2,
v(x) = ex,
v ‘ (x) = ex.
La dérivée du produit f ‘ (x) est donc la formule :
f ‘ ‘ (x) = u ‘ (x) × v(x) + u(x) × v ‘ (x)
Du coup, f ‘ ‘ (x) = 2×ex + (2x + 3)×ex
= ex × (2 + (2x + 3)) (en factorisant par l’exponentiel)
= ex × (2x + 5)
Pour déterminer le signe du produit f ‘ ‘ (x), qui a deux facteurs, on construit un tableau de signe avec chacun des facteurs.
Un exponentiel est toujours strictement positif quelque soit son contenu donc on met un unique + dans la ligne de l’exponentielle.
On met un “+” pour 2x + 5
⇔ 2x + 3 ≥ 0
⇔ 2x ≥ -5
⇔ x ≥ –5/2
⇔ on est à droite de –5/2 dans la première ligne du tableau de signe.
Donc on met le “+” à droite du “0” en dessous de –5/2.
On obtient donc le tableau suivant :
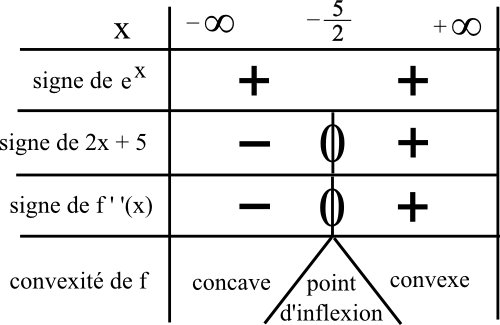
4) D’après la question précédente, le point d’inflexion est atteint en x = –5/2.
L’ordonnée de point est f(-5/2).
f(-5/2) = (2 × –5/2 + 1)e–5/2
= (-5 + 1)e–5/2
= -4e–5/2.
Les coordonnées du point d’inflexion sont donc (-5/2 ; -4e–5/2).
L’équation d’une tangente à une courbe Cf au point d’abscisse a est :

Ici, a = –5/2.
Donc f(a) = -4e–5/2
De plus,
f ‘ (a) = (2 × –5/2 + 3)e–5/2
= (-5 + 3)e–5/2
= -2e–5/2.
Du coup, l’équation de la tangente au point d’inflexion est :
y = -2e–5/2(x – (-5/2)) + (-4e–5/2)
= -2e–5/2 × x + (-2) × e–5/2 × 5/2 – 4e–5/2
= -2e–5/2 × x – 5e–5/2 – 4e–5/2
= -2e–5/2 × x – 9e–5/2
5) Convexité de g(x) = xex.
Pour trouver la convexité de g, il faut dériver deux fois et déterminer le signe de g ‘ ‘ (x).
g(x) = x × ex
= u(x) × v(x)
avec
u(x) = x,
u ‘ (x) = 1,
v(x) = ex,
v ‘ (x) = ex.
La dérivée du produit g(x) est donc la formule :
g ‘ (x) = u ‘ (x) × v(x) + u(x) × v ‘ (x)
= 1 × ex + x × ex
= ex × (1 + x).
= a(x) × b(x)
avec a(x) = ex
a ‘ (x) = ex
b(x) = 1 + x
b ‘ (x) = 1
g ‘ ‘ (x) = a ‘ (x) × b(x) + a(x) × b ‘ (x)
= ex × (1 + x) + ex × 1
= ex × (1 + x + 1)
= ex × (x + 2)
Pour déterminer le signe du produit g ‘ ‘ (x), qui a deux facteurs, on construit un tableau de signe avec chacun des facteurs.
Un exponentiel est toujours strictement positif quelque soit son contenu donc on met un unique + dans la ligne de l’exponentielle.
On met un “+” pour x + 2
⇔ x + 2 ≥ 0
⇔ x ≥ -2
⇔ x ≥ -2
⇔ on est à droite de -2 dans la première ligne du tableau de signe.
Donc on met le “+” à droite du “0” en dessous de -2.
On obtient donc le tableau suivant :
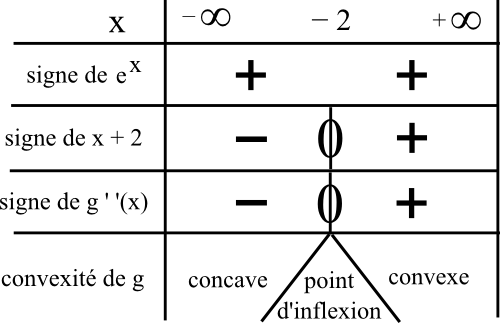
g n’est pas convexe sur R, pas concave sur R, mais admet un point d’inflexion.
6) Calculons h ‘ (x) :
h(x) = ex/(x – 1)
= u(x)/v(x)
avec u(x) = ex,
u ‘ (x) = ex,
v(x) = x – 1,
v ‘ (x) = 1.
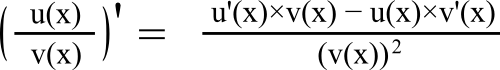
h ‘ (x) = (ex× (x – 1) – ex × 1)/(x – 1)2
= (ex(x – 2))/(x – 1)2
7) Etudions k(x) = 0,9x :
0,9 est positif, donc n’importe quelle puissance de 0,9 est positive, donc k positive sur R.
0,9 < 1 donc k (0,9x) est strictement décroissante sur R.
Tout fonction ax est convexe sur R (a > 0), k aussi.
Bonne compréhension,
Sylvain Jeuland

