Exercice : Clic droit vers l’exercice
Tout le corrigé :
1) Dérivation de f(x) = 2x3 − 3x + 2 :
Rédaction :
f(x) est un polynôme donc on dérive chaque monôme terme à terme.
f ‘(x) = 2 × 3x2 – 3 + 0
= 6x2 – 3.
2) Dérivation de g(x) = −2/x3 :
Rédaction :
On divise par x3, ce qui n’est pas facile.
Quand on a un xpositif dans un dénominateur, l’idéal est d’avoir un xnégatif au numérateur.
On utilise donc la formule suivante.
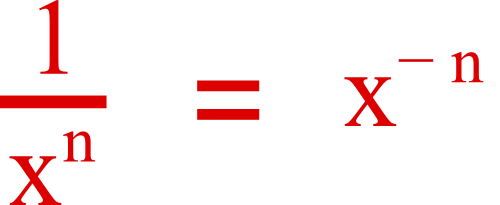
Du coup, 1/x3 = x-3.
Et −2/x3
= -2 × 1/x3
= -2 × x-3
Pour dériver ce g(x), on garde le -2 qui est un coefficient multiplicatif et on dérive le x-3 à l’aide de la formule ci-dessous.

Donc g'(x) = -2 × (-3) × x-3-1
= 6 × x-4
= 6/x4
en repassant la puissance négative au dénominateur (en exposant positif).
3) Dérivation de h(x) = 1/(3x2 + 1) :
Rédaction :
h(x) est de la forme 1/(v(x))
avec v(x) = 3x2 + 1,
donc v'(x) = 3 × 2x + 0 = 6x.
On utilise la formule suivante :
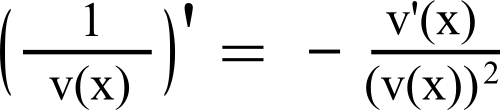
Donc h'(x) = –(v'(x))/(v(x))2
= –(6x)/(3x2 + 1)2.
4) Dérivation de i(x) = (x − 1)/(x + 1) :
Rédaction :
i(x) est de la forme (u(x))/(v(x))
avec u(x) = x − 1,
donc u'(x) = 1,
avec v(x) = x + 1,
donc v'(x) = 1.
On utilise la formule suivante de la dérivée d’un quotient :
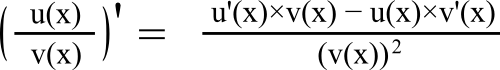
Donc i'(x) = (u'(x) × v(x) – u(x) × v'(x))/(v(x))2
= (1 × (x + 1) – 1 × (x – 1))/(x + 1)2
= ((x + 1) – (x – 1))/(x + 1)2
= (x + 1 – x + 1)/(x + 1)2
= 2/(x + 1)2.
5) Dérivation de j(x) = (x2 + 2x)/3 − 2/x :
Déjà, la première fraction, c’est un divisé par 3. Ce n’est pas un « vrai » quotient avec x en bas.
Rédaction :
j(x) = 1/3 × (x2 + 2x) − 2 × 1/x
La dérivée du polynôme « x2 + 2x » est classique.
Pour dériver 1/x, on utilise la formule suivante :
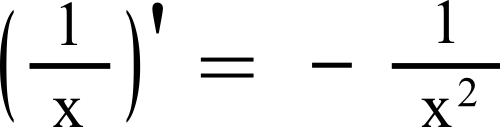
Donc j'(x) = 1/3 × (2x + 2) – 2 × (-1/x2)
= (2/3)x + 2/3 + 2/x2
6) Dérivation de k(x) = 3(x2 + 1)2 :
Rédaction :
k(x) est de la forme 3 × (u(x))2
avec u(x) = x2 + 1,
donc u'(x) = 2x.
La dérivée d’une fonction mise à la puissance n est :
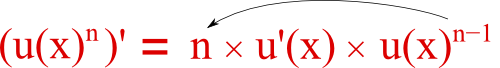
Donc k'(x) = 3 × 2 × u'(x) × (u(x))2-1
= 6 × 2x × (x2 + 1)1
= 12x × (x2 + 1)
= 12x3 + 12x.











