Maths de première : exercice d’exponentielle avec équations et dérivée. Inconnues, fonction, tangente, tableaux de signe et variation.
Exercice N°667 :
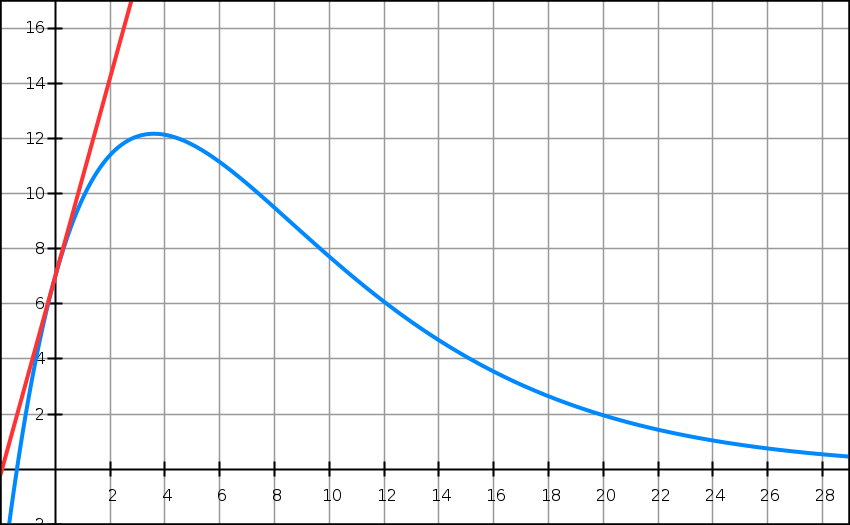
On a tracé sur le graphique ci-dessus la courbe représentative Cf d’une fonction f définie sur I = [0 ; 25] par
f(x) = (ax + b)e−0,2x
où a et b sont deux nombres réels.
On a représenté également sa tangente T au point
A(0 ; 7). T passe par le point B(2 ; 14.2).
1) Résoudre graphiquement l’équation f(x) = 6.
2) Par lecture graphique, donner f(0).
3) En déduire que sur I,
f(x) = (ax + 7)e−0,2x.
4) Quel est le coefficient directeur de la droite T ?
5) Exprimer, pour tout x appartenant à I, f ‘ (x) en fonction de a.
6) En déduire que, pour tout x appartenant à I,
f(x) = (5x + 7)e−0,2x.
On souhaite connaître le maximum de la fonction f sur I.
7) Montrer que, pour tout réel x de I,
f ‘ (x) = (−x + 3,6)e−0,2x.
8) Étudier le signe de f ‘ (x) puis les variations de f sur I.
9) En déduire le maximum de f sur I.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercices : exercice, exponentielle, équations, dérivée.
Exercice précédent : Exponentielle – Équations, inéquations, carrés, signes – Première

