Exercice : Clic droit vers l’exercice
Tout le corrigé :
1) a est l’abscisse du point, sa « largeur ».
Donc je prends 1 sur l’axe des abscisses.
f(a) est l’image, soit l’ordonnée du point, sa « hauteur ».
La courbe est en bas, donc je descends verticalement vers la courbe et je note l’ordonnée du point : c’est -4.
Donc f(1) = -4.
f ‘ (a) est la pente de la tangente de la courbe. On détermine la droite-tangente que l’on pose sur la courbe et on regarde le coefficient directeur.
Je prends le même point d’abscisse et je vois que la tangente est horizontale car on a un replat (un minimum ici) de la courbe. Donc le coefficient directeur vaut 0 car la tangente à Cf est parallèle à l’axe des abscisses (horizontale).
Donc f ‘ (1) = 0.
2) Quand la pente est positive, c’est-à-dire quand f ‘ (x) > 0, f est strictement croissante (et vice-versa).
Quand la pente est négative, c’est-à-dire quand f ‘ (x) < 0, f est strictement croissante (et vice-versa).
Quand f ‘ (x) = 0, on a un replat de Cf.
Grâce au graphique, on peut faire le tableau de variation de f, puis en déduire le signe de f ‘ (x).
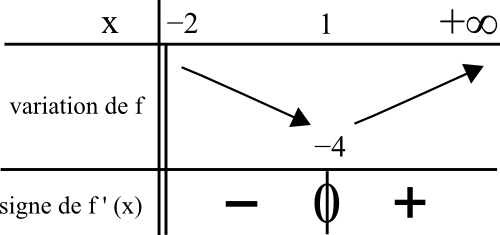
Comme f ‘ (x) est négative et devient positive après l’abscisse x = 1, seule la courbe C1 convient.
3) On a f(x) = (x2 – 6x – 7)/(x + 2).
Donc f(x) = u(x)/v(x)
avec
u(x) = x2 – 6x – 7,
u ‘ (x) = 2x – 6 – 0,
v(x) = x + 2,
v ‘ (x) = 1 + 0.
La formule de la dérivée d’un quotient est :
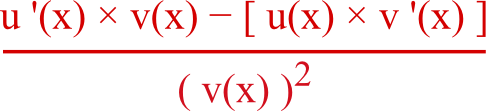
Donc Numérateur = (2x – 6) × (x + 2) – [ (x2 – 6x – 7) × 1 ]
= 2x2 + 4x – 6x – 12 – x2 + 6x + 7
= x2 + 4x – 5
Donc f ‘ (x) = (x2 + 4x – 5)/(x + 2)2
4) Pour étudier les variations de f, on détermine le signe de f ‘ (x) dans un tableau de signe. Je mets ici une ligne pour le numérateur et une ligne pour le dénominateur.
Pour le signe de x2 + 4x – 5, comme c’est un polynôme du second degré, on calcule le discriminant.
Δ = b2 – 4ac
= 42 – 4 × 1 × (-5)
= 16 + 20 = 36 > 0 soit deux racines :
x1 = (-b – √Δ)/(2a)
= (-4 – √36)/(2 × 1)
= (-4 – 6)/2
= -10/2
= -5
x2 = (-b + √Δ)/(2a)
= (-4 + √36)/(2 × 1)
= (-4 + 6)/2
= 2/2
= 1
Un polynôme du second degré est du signe de a à l’extérieur des racines quand Δ > 0 car la parabole coupe deux fois l’axe des abscisses.
Comme a = 1 > 0, la parabole « sourit » et le polynôme du second degré est positif avant -5 et après 1. Il est négatif entre -5 et 1. Puis nul entre -5 et 1.
Pour le (x + 2)2, un carré est toujours positif ou nul. Ici, il est nul en -2. Comme la fonction n’est pas définie en -2, il sera ici toujours strictement positif : on met un + dans la ligne.
Cela donne le tableau suivant :
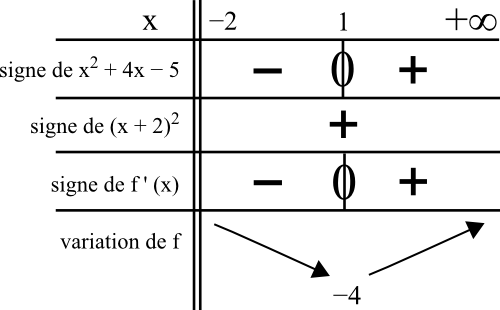
J’ai exclu l’abscisse -2 des lignes des tableaux de signe et variation. Il y a donc une double-barre à gauche.
Petit rappel pour la variation de f :
Quand la pente est positive, c’est-à-dire quand f ‘ (x) > 0, f est strictement croissante.
Quand la pente est négative, c’est-à-dire quand f ‘ (x) < 0, f est strictement decroissante.
Bonne compréhension,
Sylvain Jeuland
