Exercice de maths de terminale sur la probabilité, un arbre, suite géométrique, conditionnelles. Limite, raison, premier terme, conjecture.
Exercice N°322 :

Exercice N°322 :
Dans un zoo, l’unique activité d’un manchot est l’utilisation d’un bassin aquatique équipé d’un toboggan et d’un plongeoir.
On a observé que si un manchot choisit le toboggan, la probabilité qu’il le reprenne est 0,3.
Si un manchot choisit le plongeoir, la probabilité qu’il le reprenne est 0,8.
Lors du premier passage les deux équipements ont la même probabilité d’être choisis.
Pour tout entier naturel n non nul, on considère l’évènement :
– Tn : “Le manchot utilise le toboggan lors de son n-ième passage.”
– Pn : “Le manchot utilise le plongeoir lors de son n-ième passage.”
On considère alors la suite (un) définie pour tout entier naturel n ≥ 1 par :
un = p(Tn)
où p(Tn) est la probabilité de l’évènement Tn.
1) Donner les valeurs des probabilités p(T1), p(P1)
et des probabilités conditionnelles pT1(T2) et pP1(P2).
2) Montrer que p(T2) = 1/4.
3) Recopier et compléter l’arbre suivant :
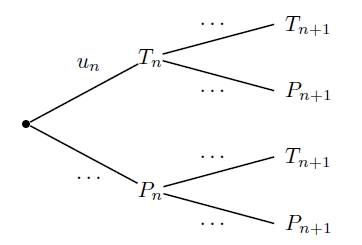
4) Démontrer que pour tout entier n ≥ 1,
un+1 = 0,1un + 0,2.
5) À l’aide de la calculatrice, émettre une conjecture concernant la limite de la suite (un).
On considère la suite (vn) définie pour tout entier naturel n ≥ 1 par :
vn = un – 2/9.
6) Démontrer que la suite (vn) est géométrique de raison 1/10. Préciser son premier terme.
7) Exprimer vn en fonction de n. En déduire l’expression de un en fonction de n.
8) Calculer la limite de la suite (un). Ce résultat permet-il de valider la conjecture émise en 5) ?
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : probabilité, arbre, suite géométrique.
Exercice précédent : Probas et Suites – Conditionnelle, arbre, géométrique – Terminale

