frenchmaths.com (par Sylvain Jeuland)

Maths de terminale : exercice d’intégrale, logarithme et suite. Fonction, variation, récurrence, fonction, continuité, limite, convergence.

Exercice N°458 :

Exercice N°458 :

On considère la fonction g définie sur l’intervalle [1 ; +∞[ par :
g(x) = ln(2x) + 1 − x.

Cette question demande le développement d’une certaine démarche comportant plusieurs étapes.
1) Démontrer que l’équation g(x) = 0 admet sur l’intervalle [1 ; +∞[ une unique solution notée α.
Donner un encadrement au centième de α.

2) Démontrer que ln(2α) + 1 = α.

Soit la suite (u_n) définie par u₀ = 1 et pour tout entier naturel n,
u_n+1 = ln(2u_n) + 1.

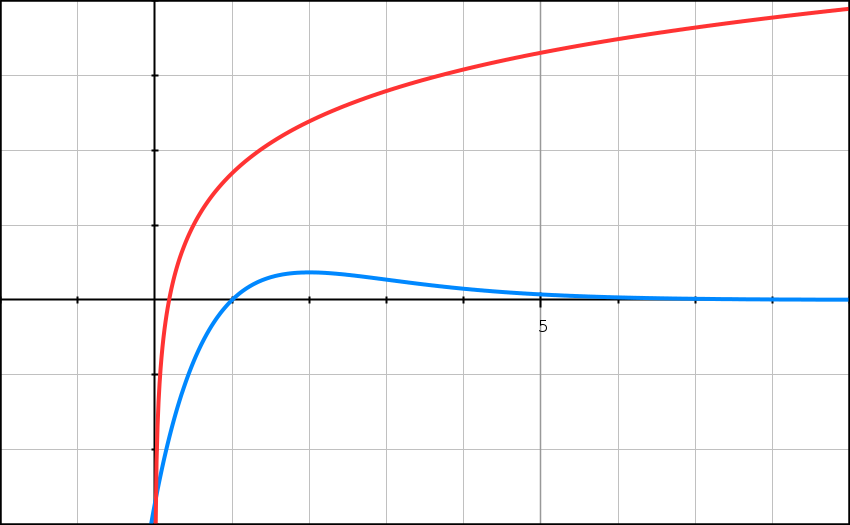
On désigne par Γ la courbe d’équation y = ln(2x) + 1 dans un repère orthonormal (O ; ^→i ; ^→j). Cette courbe est celle du haut dans le graphique des deux courbes.

3) En utilisant la courbe Γ, construire sur l’axe des abscisses les quatre premiers termes de la suite.

4) Démontrer par récurrence que pour tout entier naturel n,
1 ≤ u_n ≤ u_n+1 ≤ 3.

5) En déduire que la suite (u_n) converge vers une limite finie l ∈ [1 ; 3].

6) Démontrer que l = α.

On considère la fonction f définie sur l’intervalle [1 ; +∞[ par :
f(x) = (x − 1)e^1−x.

On désigne par C la courbe représentative de la fonction f dans un repère orthonormal (O, ^→i, ^→j). Cette courbe est celle du bas sur le graphique donné en début d’exercice.

Pour tout nombre réel x supérieur ou égal à 1, on pose :
F(x) = ∫_{[de 1 à x]} f(t)dt = ∫_{[de 1 à x]} (t − 1)e^1−tdt.

7) Démontrer que la fonction F est dérivable et croissante sur l’intervalle [1 ; +∞[.

8) Montrer que la fonction x → −x × e^1−x est une primitive de f sur l’intervalle [1 ; +∞[, en déduire que, pour tout réel x ∈ [1 ; +∞[,
F(x) = −x × e^1−x + 1.

9) Démontrer que sur l’intervalle [1 ; +∞[, l’équation
“F(x) = ¹/₂” est équivalente à l’équation “ln(2x) + 1 = x”.

Soit un réel a > 1. On considère la partie D_a du plan limité par la
courbe C, l’axe des abscisses et les droites d’équation x = 1 et x = a.

10) Déterminer le nombre a tel que l’aire, en unité d’aire, de D_a soit égale à ¹/₂ et colorier D_a sur le graphique pour cette valeur de a.

Bon courage,
Sylvain Jeuland

Mots-clés de l’exercice : exercice, intégrale, logarithme, suite.

Exercice précédent : Primitives – Intégrale, fonction, somme, encadrement – Terminale