Maths de terminale : exercice sur le logarithme népérien avec tangente, position relative, dérivée, graphique, droite et courbe.
Exercice N°422 :
Les fonctions g et h sont définies sur ]0 ; + ∞[ par
g(x) = ln(x)/(x2)
et
h(x) = ln(x).
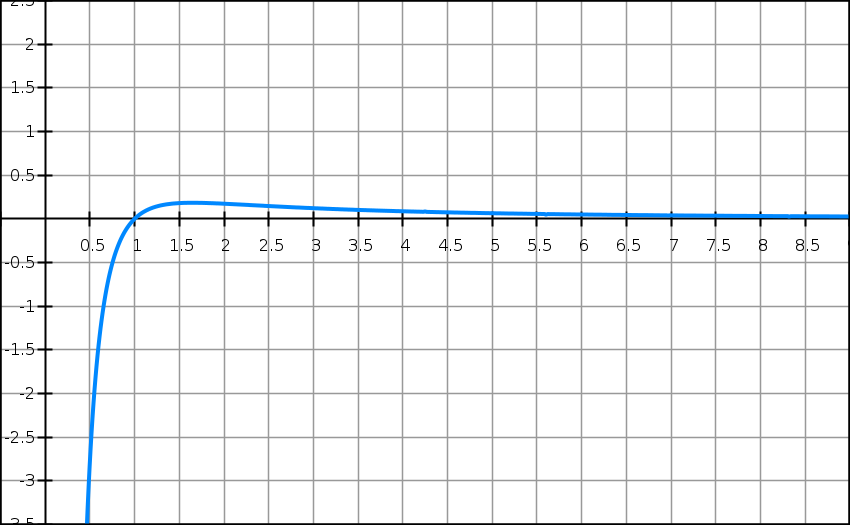
La courbe Cg a été tracée ci-dessus.
1) Étudier la position de la courbe Cg par rapport à la courbe Ch.
2) Montrer que g ‘ (x) = (1 – 2ln(x))/x3.
On note Δ la tangente à Cg au point A(1 ; 0).
3) Donner l’équation de Δ puis la tracer.
4) Montrer que Δ est aussi une tangente de la courbe Ch.
5) Montrer que Ch est située sous la droite Δ.
6) Tracer Ch sur le graphique après avoir placé quelques points.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, logarithme népérien, tangente.
Exercice précédent : Logarithme Népérien – Calculs, inéquations, dérivée – Terminale

