Exercice d’exponentielle et logarithme népérien. Maths de terminale avec équation et fonction. Variations, conjecture, tvi, courbe.
Exercice N°354 :
On considère l’équation (E) d’inconnue x réelle :
ex = 3(x2 + x3).
Le graphique ci-dessous donne la courbe représentative de la fonction exponentielle et celle de la fonction f définie sur R par
f(x) = 3(x2 + x3)
telles que les affiche une calculatrice dans un même repère orthogonal.
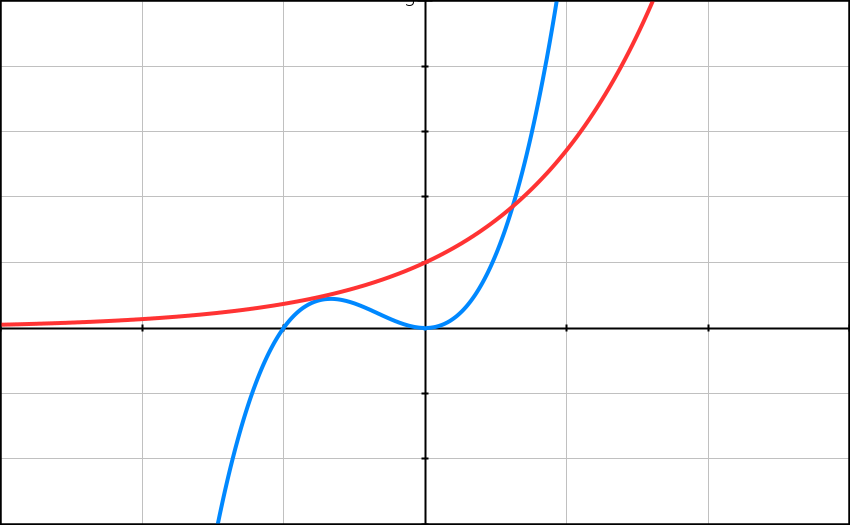
1) A l’aide du graphique ci-dessus, conjecturer le nombre de solutions de
l’équation (E) et leur encadrement par deux entiers consécutifs.
2) Étudier selon les valeurs de x, le signe de
x2 + x3.
3) En déduire que l’équation (E) n’a pas de solution sur l’intervalle ]-∞ ; −1].
4) Vérifier que 0 n’est pas solution de (E).
On considère la fonction h, définie pour tout nombre réel de
]−1 ; 0[⋃]0 ; +∞[ par :
h(x) = ln 3 + ln (x2) + ln(1 + x) − x.
5) Montrer que, sur ]−1 ; 0[⋃]0 ; +∞[, l’équation (E) équivaut à
h(x) = 0.
6) Montrer que, pour tout réel x appartenant à ]−1 ; 0[⋃]0 ; +∞[, on a :
h ‘ (x) = (−x2 + 2x + 2)/x(x + 1).
7) Déterminer les variations de la fonction h.
8) Déterminer le nombre de solutions de l’équation h(x) = 0 et donner une valeur arrondie au centième de chaque solution.
9) Conclure quant à la conjecture de la question 1).
Bon courage,
Sylvain Jeuland
Questions 1-2-3 : Clic droit vers le corrigé
Pour avoir le corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de ce chapitre (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés de l’exercice : exercice, exponentielle, logarithme népérien.
Exercice précédent : Logarithme Népérien – Fonction, variation, distance – Terminale

