Exercice de maths de terminale sur le bac 2016 sur la fonction, intégrale, primitive, logarithme népérien, dérivée, variation, TVI, surface.
Exercice N°600 :

Exercice N°600 :
La courbe (C) ci-dessous représente, dans un repère orthonormé, une fonction f définie et dérivable sur [0.5 ; 6]. Les points A(1 ; 3) et B d’abscisse 1,5 sont sur la courbe (C).
Les tangentes à la courbe (C) aux points A et B sont aussi représentées en pointillés sur ce graphique, la tangente au point B est horizontale.
On note f ‘ la fonction dérivée de f.
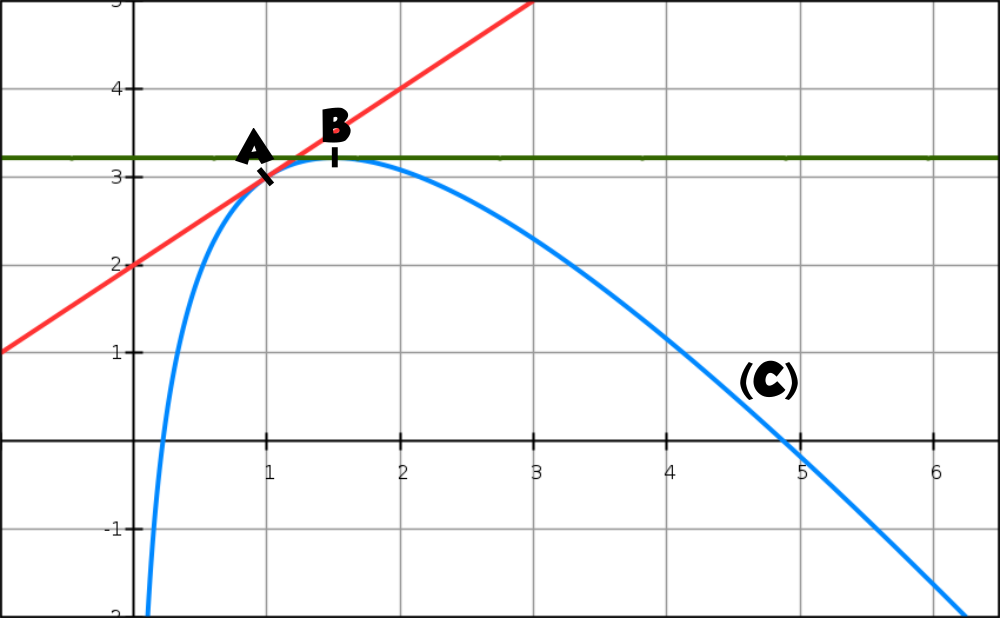
Les parties A et B sont indépendantes.
Partie A : Étude graphique
1) Déterminer f ‘ (1,5).
La tangente à la courbe (C) au point A passe par le point de coordonnées (0 ; 2).
2) Déterminer une équation de cette tangente.
3) Donner un encadrement de l’aire, en unités d’aire et à l’unité près, du domaine compris entre la courbe (C), l’axe des abscisses et les droites d’équation x = 1 et x = 2.
4) Déterminer la convexité de la fonction sur [0,5 ; 6]. Argumenter la réponse.
Partie B : Étude analytique
On admet que la fonction f est définie sur [0,5 ; 6] par
f(x) = −2x + 5 + 3ln(x).
5) Pour tout réel de [0,5 ; 6], calculer f ‘ (x)
et montrer que f ‘ (x) = (-2x + 3)/x.
6) Étudier le signe de f ‘ (x) sur [0,5 ; 6] puis dresser le tableau de variation de f sur [0,5 ; 6].
7) Montrer que l’équation f(x) = 0 admet exactement une solution α sur [0,5 ; 6].
Donner une valeur approchée de α à 10-2 près.
8) En déduire le tableau de signe de f sur [0,5 ; 6].
On considère la fonction F définie sur [0,5 ; 6]
par F(x)= −x2 + 2x + 3xln(x).
9) Montrer que F est une primitive de f sur [0,5 ; 6].
10) En déduire l’aire exacte, en unités d’aire, du domaine compris entre la courbe (C), l’axe des abscisses et les droites d’équation x = 1 et x = 2. En donner ensuite une valeur arrondie au dixième.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : intégrale, primitive, logarithme népérien.
Exercice précédent : Second degré – Sommet, équations, canonique, factorisée – Première

