Exercice : Clic droit vers le corrigé
Tout le corrigé :
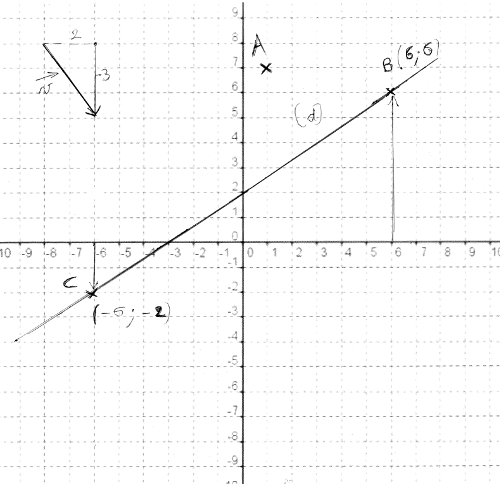
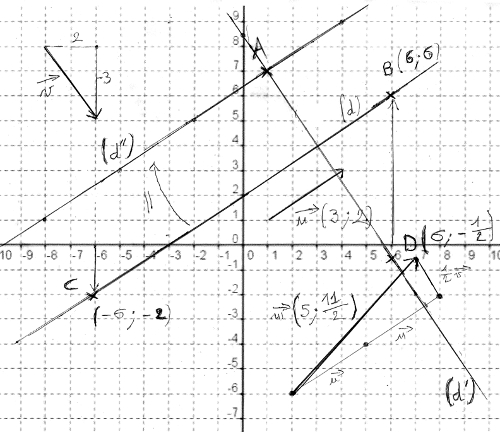
1) (d), A et →v :
Rédaction :
Comme →v est un vecteur, on peut le placer n’importe où sur le repère. Je prends un point de départ et je vais de 2 vers la droite (x = 2) et de 3 vers le bas (y = -3).
Pour tracer la droite, on choisit deux abscisses espacés et on calcule y.
Je choisis x = 6 et x = -6.
Pour x = 6 :
L’équation de droite est : 2x – 3y + 6 = 0
⇔ 2 × 6 – 3y + 6 = 0
⇔ 12 – 3y + 6 = 0
⇔ 18 – 3y = 0
⇔ 18 = 3y
⇔ 6 = y
Les coordonnées de B, premier point de la droite (d) sont (6 ; 6).
Pour x = -6 :
2x – 3y + 6 = 0
⇔ 2 × (-6) – 3y + 6 = 0
⇔ -12 – 3y + 6 = 0
⇔ -6 – 3y = 0
⇔ -6 = 3y
⇔ -2 = y
Les coordonnées de C, second point de la droite (d) sont (-6 ; -2).
Je place ces deux points sur le graphique. Et je trace l’unique droite qui passe par ces deux points. Pour vérifier, je remplace x par 0 pour voir qu’elle est l’ordonnée à l’origine.
Soit 2 × 0 – 3y + 6 = 0
⇔ –3y + 6 = 0
⇔ 6 = 3y
⇔ 2 = y
C’est bon car on voit bien que la droite passe par l’ordonnée 2 sur l’axe des ordonnées. Il n’y a pas de contradiction.
2) Vecteur →u directeur de (d) :
Rédaction :
Les coordonnées d’un des vecteurs directeurs d’une droite sont :
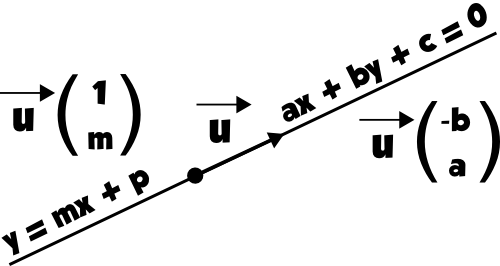
Comme l’équation de droite est 2x – 3y + 6 = 0,
a = 2 et b = (-3).
Le vecteur directeur (le plus simple) est donc ->u(-b ; a) donc →u(-(-3) ; 2). Du coup, le vecteur directeur de (d) →u a pour coordonnées (3 ; 2).
3) →w = 2→u – 1/2→v :
Rédaction :
Je place un point de départ sur la partie basse à droite. A partir de ce point, je fais deux fois le vecteur →u puis la moitié de →v à l’envers. J’obtiens un point d’arrivée. Du coup, j’ai le déplacement vecteur →w.
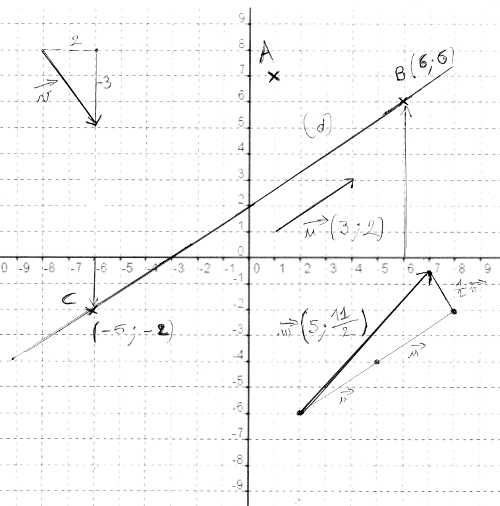
4) Calculer ensuite les coordonnées de →w :
Rédaction :
Cette question dépend du résultat trouvé à la question précédente.
Comme →w = 2→u – 1/2→v,
l’abscisse x→w = 2x→u – 1/2x→v
= 2 × 3 – 1/2 × 2
= 6 – 1 = 5.
Et l’ordonnée y→w = 2y→u – 1/2y→v
= 2 × 2 – 1/2 × (-3)
= 4 + 1,5 = 5,5 = 11/2.
Donc →w(5 ; 11/2).
5) Colinéarité :
Rédaction :
Là encore, cela dépend du vecteur directeur →u trouvé au départ. Regardons si les coordonnées de →v et de →w sont proportionnelles.
x = 2 et y = -3.
x’ = 5 et y’ = 11/2.
On a donc le tableau :
2 | -3
5 | 11/2
Les produits en croix sont :
2 × 11/2 = 11
Et :
5 × -3 = -15
Donc les produits en croix sont différent, x’y – xy’ est différent de 0, les coordonnées ne sont pas proportionnelles, donc les vecteurs →v et →w ne sont pas colinéaires.
6) Équation de (d’) passant par A et de vecteur →v :
Rédaction :
On veut une équation cartésienne donc du type ax + by + c = 0.
Comme →v est un vecteur directeur. Ses coordonnées 2 et -3 sont -b et a. Du coup, -b = 2 (b = -2) et a = -3.
L’équation s’écrit donc -3x – 2y + c = 0.
Pour déterminer le nombre c, on remplace x et y par les coordonnées de A car ce point est sur la droite.
-3xA – 2yA + c = 0
⇔ -3xA – 2yA + c = 0
⇔ -3 × 1 – 2 × 7 + c = 0
⇔ -3 – 14 + c = 0
⇔ -17 + c = 0
⇔ c = 17.
Donc une équation cartésienne de droite est -3x – 2y + 17 = 0.
On sait que (d’) passe par A. Je choisis un autre abscisse x pour trouver un second point de la droite pour la tracer.
Je prends x = 6.
-3x – 2y + 17 = 0
⇔ -3 × 6 – 2y + 17 = 0
⇔ -18 – 2y + 17 = 0
⇔ -1 – 2y = 0
⇔ -1 = 2y
⇔ -1/2 = y
Le second point de la droite, E, a pour coordonnées (6 ; -1/2).
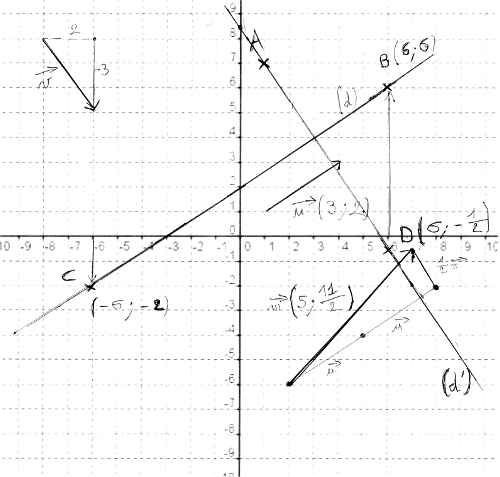
Si on remplace x par 0, on peut calculer que y = 8,5. Ce qui correspond à l’ordonnée à l’origine que l’on peut voir sur le dessin.
7) Intersection de (d) et (d’) :
Rédaction :
Pour déterminer les coordonnées x et y du point d’intersection de deux droites, on utilise les équations de ces deux droites. En effet, les coordonnées du point d’intersection respecte à la fois ces deux égalités. Cela fait donc un système à résoudre pour trouver le x et le y.
{ 2x – 3y + 6 = 0 pour (d)
{ -3x – 2y + 17 = 0 pour (d’)
Ces deux accolades sont en fait une seule grande accolade.
La première étape pour résoudre un système est d’obtenir le même nombre de x (ou de y) sur chaque ligne.
Ici j’ai 2x et -3x, donc je multiplie la première ligné par 3 et la second par -2 pour obtenir 6x et 6x.
⇔
{ 6x – 9y + 18 = 0
{ 6x + 4y – 34 = 0
Ensuite, j’isole les x à gauche et j’envoie le reste à droite du égal.
⇔
{ 6x = 9y – 18
{ 6x = -4y + 34
Comme 6x = 6x, cela veut dire que 9y – 18 = -4y + 34.
⇔
{ 9y – 18 = -4y + 34
{ 6x = 9y – 18
{ 6x = -4y + 34
Du coup, je résous cette équation.
9y – 18 = -4y + 34 équivaut à 13y = 52 et donc y = 4 (en divisant par 13).
Revenons au système :
⇔
{ y = 4
{ 6x = 9 × 4 – 18 = 18
{ 6x = -4 × 4 + 34 = 18
⇔
{ y = 4
{ x = 18/6 = 3.
⇔
Le point d’intersection I a pour coordonnées (3 ; 4).
8) Équation cartésienne de la droite (d ‘ ‘) :
Rédaction :
Lorsqu’on veut une droite parallèle, il suffit de garder le même “a” et le même “b”.
Comme (d) a pour équation 2x – 3y + 6 = 0,
on peut aussi choisir 2 et -3 pour (d ‘ ‘).
Du coup, (d ‘ ‘) a pour équation 2x – 3y + c = 0.
Pour déterminer le c, on peut remplacer par un point de la droite, ici A(1 ; 7).
Donc 2 × 1 – 3 × 7 + c = 0.
⇔ 2 – 21 + c = 0.
⇔ -19 + c = 0
⇔ c = 19
L’équation de (d ‘ ‘) est donc 2x – 3y + 19 = 0.
Je trace la parallèle à (d) passant par A.
Bonne compréhension,
Sylvain Jeuland

